Cho đẳng thức: x 2 − 1 ( x 2 − 2 x + 1 ) = x + 1 ( x 2 − x − 6 ) B với x ≠ − 2 ; 1 ; 3 .
Hãy tìm một cặp đa thức A và B thỏa mãn đẳng thức trên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
19 tháng 11 2018
Đúng(0)
Những câu hỏi liên quan
17 tháng 7 2020
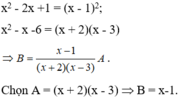
Câu 1:
a) Ta có: \(VT=x^4-y^4\)
\(=\left(x^2-y^2\right)\left(x^2+y^2\right)\)
\(=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
\(=\left(x-y\right)\left(x^3+xy^2+x^2y+y^3\right)\)=VP(đpcm)
c) Ta có: \(VT=a\left(b+1\right)+b\left(a+1\right)\)
\(=ab+a+ab+b\)
\(=a+b+2ab\)(1)
Thay ab=1 vào biểu thức (1), ta được:
a+b+2(*)
Ta có: VP=(a+1)(b+1)=ab+a+b+1(2)
Thay ab=1 vào biểu thức (2), ta được:
1+a+b+1=a+b+2(**)
Từ (*) và (**) ta được VT=VP(đpcm)
Câu 2:
Ta có: \(\left(x-3\right)\left(x+x^2\right)+2\left(x-5\right)\left(x+1\right)-x^3=12\)
\(\Leftrightarrow x^2+x^3-3x-3x^2+2\left(x^2+x-5x-5\right)-x^3=12\)
\(\Leftrightarrow x^3-2x^2-3x+2x^2-8x-10-x^3-12=0\)
\(\Leftrightarrow-11x-22=0\)
\(\Leftrightarrow-11x=22\)
hay x=-2
Vậy: x=-2
DH
1
DT
11 tháng 6 2019
Theo đề ra :\(x^2+y^2=2\Leftrightarrow x^2+y^2+2xy=2+2xy\Leftrightarrow\left(x+y\right)^2=2+2xy.\)(1)
Khi đó \(\left(x+y\right)\left(x+y+2\right)=\left(x+y\right)^2+2\left(x+y\right)\)
\(=2+2xy+2\left(x+y\right)\)( Thế (1) vô)
\(=2\left(x+y+xy+1\right)\)
\(=2\left[y\left(x+1\right)+\left(x+1\right)\right]\)
\(=2\left(x+1\right)\left(y+1\right)\)
NN
1
NT
1
19 tháng 6 2019
Bạn ơi đề bài sai nha mik sửa lại đề bài
\(\left(x^3-1\right)\left(x^3+1\right)=\left(x^2-1\right)\left(x^2+x+1\right)\)
VT = \(\left(x^3-1\right)\left(x^3+1\right)=\left(x^3\right)^2-1=x^6-1\)
VP = \(\left(x^2-1\right)\left(x^2+x+1\right)=\left(x^2\right)^3-1=x^6-1\)
Ta thấy VT = VP
=> \(\left(x^3-1\right)\left(x^3+1\right)=\left(x^2-1\right)\left(x^2+x+1\right)\) (đpcm)
N
0
1 tháng 12 2021
1. không đáp án đúng
2.\(\dfrac{1}{y-x}\sqrt{2x^2\left(x-y\right)^2}=\dfrac{-1}{x-y}x\left(x-y\right)\sqrt{2}\left(vì>y>0\right)=-x\sqrt{2}\)
NT
1
16 tháng 7 2022
\(\left(x+y\right)\left(x+y+2\right)\)
\(=\left(x+y\right)^2+2\left(x+y\right)\)
\(=x^2+y^2+2xy+2\left(x+y\right)\)
\(=2+2xy+2\left(x+y\right)\)
\(=2\left(xy+x+y+1\right)\)
\(=2\left(x+1\right)\left(y+1\right)\)
TT
1
U
1