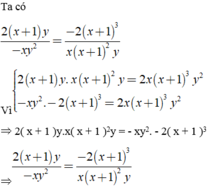Chứng minh các cặp phân thức sau bằng nhau và
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(a,VP=\dfrac{x^2+4x+3}{x^2+6x+9}=\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x+3\right)^2}=\dfrac{x+1}{x+3}=VT\)
Vậy ta có đpcm
b, \(VP=\dfrac{3x\left(x+y\right)^2}{9x^2\left(x+y\right)}=\dfrac{x+y}{3x}=VT\)
Vậy ta có đpcm
a) Ta có: \(\dfrac{x^2+4x+3}{x^2+6x+9}\)
\(=\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x+3\right)\left(x+3\right)}\)
\(=\dfrac{x+1}{x+3}\)
b: Ta có: \(\dfrac{3x\left(x+y\right)^2}{9x^2\left(x+y\right)}\)
\(=\dfrac{3x\left(x+y\right)\left(x+y\right)}{3x\cdot3x\cdot\left(x+y\right)}\)
\(=\dfrac{x+y}{3x}\)

4,Gọi ƯC(21n+4;14n+3) là d
Ta có:+>21n+4 chia hết cho d
+>14n+3 chia hết cho d
=>2(21n+4) chia hết cho d
3(14n+3) chia hết cho 3
=>42n+8 chia hết cho d
42n+9 chia hết cho d
=>(42n+9)-(42n+8) chia hết cho d
=> 42n+9-42n-8 chia hết cho d
=>1 chia hết cho d
=> d thuộc Ư(1)={1}
Mà hai số có ƯCLN=1 thì nguyên tố cùng nhau
=> 21n+4 /14n+3 là phân số tối giản(đpcm)
Vậy 21n+4/14n+3 là phân số tối giản

\(\left(x-y\right)^3+4y\left(2x^2+y^2\right)=\left(x+y\right)^3+2y\left(x^2+y^2\right)\)
\(\Leftrightarrow x^3-3x^2y+3xy^2-y^3+8x^2y+4y^3=x^3+3x^2y+3xy^2+y^3+2x^2y+2y^3\)
\(\Leftrightarrow\left(-3x^2y+8x^2y\right)+3xy^2+3y^3=\left(3x^2y+2x^2y\right)+3xy^2+3y^2\)
\(\Leftrightarrow5x^2y+3xy^2+3y^2=5x^2y+3xy^2+3y^2\)