Tập nghiệm của bất phương trình là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)

a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình  không thể có nghiệm x = - 1
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 

Đáp án: B
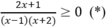
Ta có bảng xét dấu vế trái của (*):
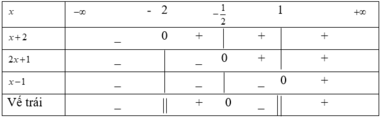
Từ đó suy ra tập nghiệm của (*) là:

Đoán đề: \(\dfrac{x^2-1}{\left(x+1\right)\left(x^2-x-6\right)}\ge0\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x-3\right)\left(x+2\right)}\ge0\)
Xét x-1=0 <=> x=1
x+1=0 <=> x=-1
x-3=0 <=> x=3
x+2=0 <=>x=-2
Bảng xét dấu:
x -2 -1 1 3 -vc +vc x-1 x+2 x-3 x+1 VT 0 0 0 0 0 + + + + - - - - + + + + + - - - - - - + + + - + - - +
Để VT \(\ge0\) <=> x\(\in\left(-2;-1\right)\cup\left(3;+\infty\right)\cup\left\{1\right\}\)

Tập nghiệm của bất phương trình đã cho là đoạn [2a - b + 1; -a + 2b - 1] (nếu 2a - 6 + 1 ≤ -a + 26 - 1) hoặc là đoạn [-a + 26 - 1 ; 2a - 6 + 1] (nếu -a + 2b - 1 ≤ 2a - 6 - 1)
Do đó để tập nghiệm của bất phương trình đã cho là đoạn [0;2], điều kiện cần và đủ là:
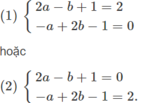
Giải (1) ta được a = b = 1. Giải hệ (2) ta được a = 1/3, b = 5/3
Đáp số: a = b = 1 hoặc a = 1/3, b = 5/3
Chọn D.
Điều kiện: x ≠ -2;1
Khi đó, ta có:
Lập bảng xét dấu.
Tập nghiệm của bất phương trình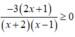 là
là 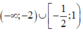 .
.