Question

[Pham Trong Bach]

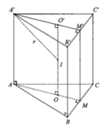
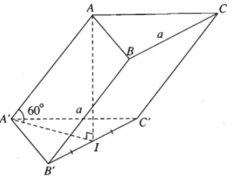
Tính chất nào sau đây không phải là tính chất của hình lăng trụ đứng:

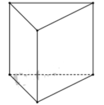
A. Các mặt bên của hình lăng trụ đứng vuông góc với nhau

B. Các mặt bên của hình lăng trụ đứng là những hình chữ nhật

C. Các cạnh bên của hình lăng trụ đứng bằng nhau và song song với nhau

D. Hai đáy của hình lăng trụ đứng có các cạnh tương ứng song song và bằng nhau

Answer 1

[Cao Minh Tâm]

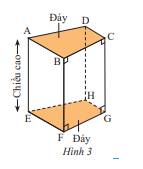
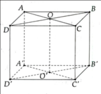
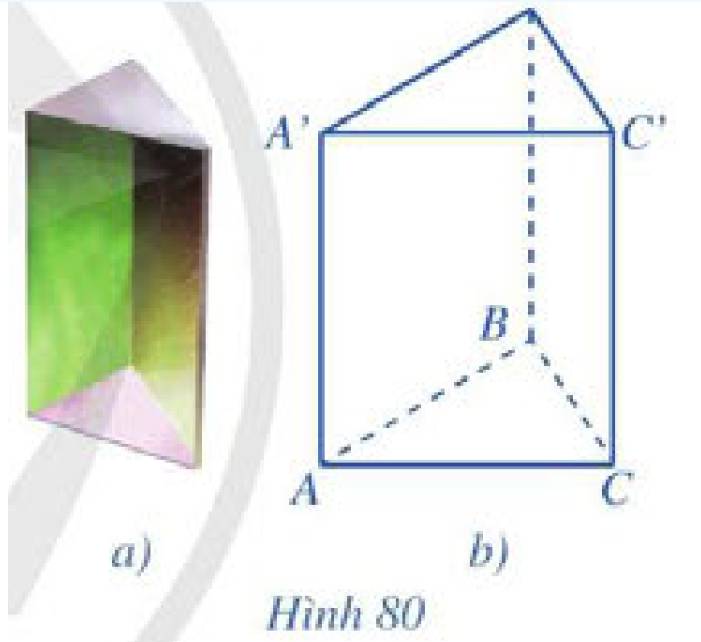
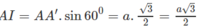
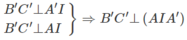
Đáp án A

- Phương pháp: Hình lăng trụ đứng là lăng trụ có cạnh bên vuông góc với đáy.

- Cách giải: Các cạnh bên của lăng trụ đứng cùng vuông góc với đáy nên chúng song song với nhau, do đó đáp án A sai