Giải các bất phương trình logarit sau: 1 5 - logx + 2 1 + log x < 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TV
0
PT
1
PT
1
CM
1 tháng 11 2018
Với điều kiện x > 0, ta có
log x + 2 log x = log9 + log x
⇔ logx = log3 ⇔ x = 3
CM
30 tháng 1 2018
Điều kiện x > 1. Khi đó phương trình tương đương với
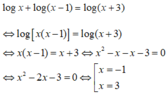
Loại nghiệm x = -1 do không thỏa mãn điều kiện. Phương trình có một nghiệm x = 3.
Chọn đáp án B.
CM
17 tháng 12 2017
Điều kiện x > 0. Khi đó bất phương trình đã cho tương đương với
log[x(x + 9)] > 1 ⇔ x(x + 9) > 10 ⇔ x 2 + 9 x - 10 > 0
⇔ x < -10 hoặc x > 1 ⇔ x > 1 (do x > 0)
Chọn A
PT
1
PT
1
CM
11 tháng 3 2018
a) Bất phương trình đã cho tương đương với hệ sau:
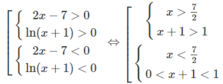
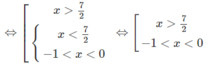
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
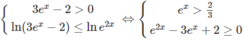
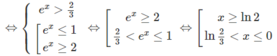
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )
PT
1
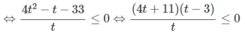
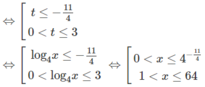
Đặt t = logx với điều kiện t ≠ 5, t ≠ −1 ta có:
Suy ra log x < -1 hoặc 2 < log x < 3 hoặc log x > 5.
Vậy x < 1/10 hoặc 100 < x < 1000 hoặc x > 100 000.