Cho hàm số y = 1 3 x 3 - 2 x 2 + 2 x + 1 C . Biết đồ thị (C) có hai tiếp tuyến cùng vuông góc với đường thẳng d: y = x. Gọi h là khoảng cách giữa hai tiếp tuyến đó. Tính h.
A. h = 2
B. h = 4 2 3
C. h = 2 3
D. h = 2 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=3x^2+6x-6\)
Tiếp tuyến vuông góc đường thẳng đã cho nên có hệ số góc thỏa mãn:
\(k.\left(-\dfrac{1}{18}\right)=-1\Rightarrow k=18\)
\(\Rightarrow3x^2+6x-6=18\Rightarrow\left[{}\begin{matrix}x=2\Rightarrow y=9\\x=-4\Rightarrow y=9\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=18\left(x-2\right)+9\\y=18\left(x+4\right)+9\end{matrix}\right.\)

Từ giả thiết suy ra tiếp tuyến có hệ số góc bằng -1
Hai tiếp điểm có hoành độ là nghiệm của phương trình y ' x 0 = - 1
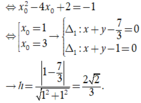
Chọn C.

\(y=x^3-3x^2+2x+2\Rightarrow y'=3x^2-6x+2\)
Vi \(\Delta\perp d:y=x-3\Rightarrow y'=-1\Leftrightarrow3x^2-6x+2=-1\)
\(\Rightarrow x=1\Rightarrow y=1-3+2+2=2\)
\(\Rightarrow\Delta:y=-1\left(x-1\right)+2\)

a.
\(y'=\dfrac{\left(sinx+cosx\right)'}{2\sqrt{sinx+cosx}}=\dfrac{cosx-sinx}{2\sqrt{sinx+cosx}}\)
b.
\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
Tiếp tuyến vuông góc với \(y=\dfrac{1}{4}x+5\) nên có hệ số góc thỏa mãn \(k.\left(\dfrac{1}{4}\right)=-1\Rightarrow k=-4\)
\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left(x-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-3\\x=2\Rightarrow y=5\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4x-3\\y=-4\left(x-2\right)+5\end{matrix}\right.\)

\(y'=8x^3-8x\)
a. Đường thẳng \(x-48y+1=0\) có hệ số góc \(\dfrac{1}{48}\) nên tiếp tuyến có hệ số góc \(k=-48\)
\(\Rightarrow8x^3-8x=-48\Rightarrow x^3-x+6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+3\right)=0\Rightarrow x=-2\)
\(y'\left(-2\right)=47\)
Phương trình tiếp tuyến: \(y=-48\left(x+2\right)+47\)
b. Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\left(8x_0^3-8x_0\right)\left(x-x_0\right)+2x^4_0-4x^2_0-1\) (1)
Do tiếp tuyến qua A:
\(\Rightarrow-3=\left(8x_0^3-8x_0\right)\left(1-x_0\right)+2x_0^4-4x^2_0-1\)
\(\Leftrightarrow3x_0^4-4x_0^3-2x_0^2+4x_0-1=0\)
\(\Leftrightarrow\left(x_0-1\right)^2\left(3x_0^2+2x_0-1\right)=0\Rightarrow\left[{}\begin{matrix}x_0=1\\x_0=-1\\x_0=\dfrac{1}{3}\end{matrix}\right.\)
Có 3 tiếp tuyến thỏa mãn. Thay lần lượt các giá trị \(x_0\) bên trên vào (1) là được
Đáp án D
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; y0) là: y = f'(x0).(x - x0) + y0
Cách giải:
Tiếp tuyến của (C) vuông góc với đường thẳng d: y = x nên tiếp tuyến có hệ số góc k = -1
=> Phương trình tiếp tuyến
=> Phương trình tiếp tuyến