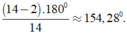Cho đa giác đều có 14 cạnh. Tính: Số đo một góc của đa giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
1 tháng 1 2018
Số đo của một góc của đa giác đều n cạnh là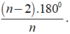
Số đo một góc của đa giác 14 cạnh là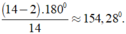
PT
1
PT
1
CM
10 tháng 5 2019
Tổng số đo các góc của đa giác n cạnh là ( n - 2 ) . 180 0 .
Tổng số đo của đa giác 14 cạnh là ( 14 - 2 ) . 180 0 = 2160 0 .
PT
1
CM
2 tháng 10 2019
Hướng dẫn:
+ Số đo của một góc của đa giác đều n cạnh là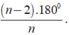
Khi đó số đo của một góc của đa giác đều 20 cạnh là:
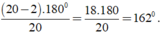
+ Số đường chéo của đa giác n cạnh là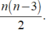
Khi đó số đường chéo của đa giác đều 20 cạnh là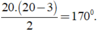
TL
3
20 tháng 9 2019
Gọi số cạnh là n
Ta có công thức tính mỗi góc của đa giác đều n cạnh là :
\(\frac{\left(n-2\right).180^0}{n}\)
CC
20 tháng 9 2019
Đa giác đều có số đường chéo bằng số cạnh
\(\Rightarrow\)Đa giác đều đó là tam giác đều và tổng số đo mỗi góc là \(60^o\)
25 tháng 12 2017
a) Số đường chéo của đa giác đó :
\(\frac{\left(8-3\right).8}{2}=20\)( đường chéo )
b) Tổng số đo các góc của đa giác là :
\(108.\left(8-2\right)=108.6=1080\)độ
c) Số đo mỗi góc của đa giác đều 8 cạnh :
\(1080:8=135\)độ
CM
2 tháng 10 2017
Gọi n là số cạnh của đa giác đều cần tìm (n ≥ 3)
Mỗi góc trong của đa giác đều có số đo
( n − 2 ) 180 ° n
Tổng số đo các góc ngoài của một đa giác là 3600
Theo bài ra ta có phương trình:
3600 + ( n − 2 ) 180 ° n = 4680
ó = 4680 - 3600
ó = 1080
ó 1800.n – 3600 = 1080 .n
ó 1800.n – 1080 .n = 3600
ó 720.n = 3600
ó n = 3600: 720
ó n = 5
Vậy đa giác đề cần tìm có 5 cạnh.
Đáp án cần chọn là: A
CM
10 tháng 7 2018
Gọi n là số cạnh của đa giác đều cần tìm (n ≥ 3)
Mỗi góc của đa giác đều có số đo
( n − 2 ) 180 ° n
Tổng số đo các góc ngoài của một đa giác là 3600
Theo bài ra ta có phương trình:
3600 + ( n − 2 ) 180 ° n = 4800
ó = 4800 - 3600
ó = 1200
ó 1800.n – 3600 = 1200 .n
ó 1800.n – 1200 .n = 3600
ó 600.n = 3600
ó n = 3600: 600
ó n = 6
Vậy đa giác đề cần tìm có 6 cạnh.
Đáp án cần chọn là: C
Số đo của một góc của đa giác đều n cạnh là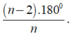
Số đo một góc của đa giác 14 cạnh là