Cho I = ∫ 0 1 ( ax - e x ) dx . Xác định a để I < 1+ 2e
A. a < 6e
B. a < 4e
C. a > 4e
D. a > 6e
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
27 tháng 10 2017
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
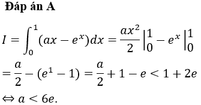
a) \(A \cup B = \{ a;b;c;d;e;i;u\} \), \(A \cap B = \{ a;e\} \)
b) Phương trình \({x^2} + 2x - 3 = 0\) có hai nghiệm là 1 và -3, nên \(A = \{ 1; - 3\} \)
Phương trình \(B = \{ x \in \mathbb{R}|\;|x|\; = 1\} \) có hai nghiệm là 1 và -1, nên \(B = \{ 1; - 1\} \)
Từ đó, \(A \cup B = \{ 1; - 1; - 3\} \), \(A \cap B = \{ 1\} .\)
30 tháng 4 2020
Câu c với f là mình sửa lại nhé, chắc gõ nhầm :v
Bài 1:
a, ab + ac
= a(b + c)
b, ab - ac + a
= a(b - c + 1)
c, ax - b - (x + ax)
= ax - b - x - ax
= -b - x
= -1(b + x)
d, a(b + c) - d(b + c)
= (b + c)(a - d)
e, ac - ad + bc - bd
= a(c - d) + b(c - d)
= (c - d)(a + b)
f, ax + by + bx + ay
= a(x + y) + b(x + y)
= (x + y)(a + b)
Bài 2:
a, n + 7 \(⋮\) n + 2 (n \(\ne\) -2)
n + 2 + 5 \(⋮\) n + 2
Mà n + 2 \(⋮\) n + 2
\(\Rightarrow\) 5 \(⋮\) n + 2
\(\Rightarrow\) n + 2 \(\in\) Ư(5) = {-1; 1; -5; 5}
Xét các TH:
n + 2 = -1 \(\Rightarrow\) n = -3 (TM)
n + 2 = 1 \(\Rightarrow\) n = -1 (TM)
n + 2 = -5 \(\Rightarrow\) n = -7 (TM)
n + 2 = 5 \(\Rightarrow\) n = 3 (TM)
Vậy n \(\in\) {-3; -1; -7; 3}
b, 9 - n \(⋮\) n - 3 (n \(\ne\) 3)
6 - (n - 3) \(⋮\) n - 3
Mà n - 3 \(⋮\) n - 3
\(\Rightarrow\) 6 \(⋮\) n - 3
\(\Rightarrow\) n - 3 \(\in\) Ư(6) = {1; -1; 2; -2; 3; -3; 6; -6}
Xét các TH:
n - 3 = 1 \(\Rightarrow\) n = 4 (TM)
n - 3 = -1 \(\Rightarrow\) n = 2 (TM)
n - 3 = 2 \(\Rightarrow\) n = 5 (TM)
n - 3 = -2 \(\Rightarrow\) n = 1 (TM)
n - 3 = 3 \(\Rightarrow\) n = 6 (TM)
n - 3 = -3 \(\Rightarrow\) n = 0 (TM)
n - 3 = 6 \(\Rightarrow\) n = 9 (TM)
n - 3 = -6 \(\Rightarrow\) n = -3 (TM)
Vậy n \(\in\) {4; 2; 5; 1; 6; 0; 9; -3}
c, 2n + 7 \(⋮\) n + 1 (n \(\ne\) -1)
2n + 2 + 5 \(⋮\) n + 1
2(n + 1) + 5 \(⋮\) n + 1
Ta có: n + 1 \(⋮\) n + 1 nên 2(n + 1) \(⋮\) n + 1
\(\Rightarrow\) 5 \(⋮\) n + 1
\(\Rightarrow\) n + 1 \(\in\) Ư(5) = {1; -1; 5; -5}
Xét 4 TH:
n + 1 = -1 \(\Rightarrow\) n = -2 (TM)
n + 1 = 1 \(\Rightarrow\) n = 0 (TM)
n + 1 = -5 \(\Rightarrow\) n = -6 (TM)
n + 1 = 5 \(\Rightarrow\) n = 4 (TM)
Vậy n \(\in\) {-2; 0; -6; 4}
d, 3n + 7 \(⋮\) 2n + 1 (n \(\ne\) \(\frac{-1}{2}\))
Vì 3n + 7 \(⋮\) 2n + 1 nên 2(3n + 7) \(⋮\) 2n + 1 hay 6n + 14 \(⋮\) 2n + 1
Ta có: 6n + 14 \(⋮\) 2n + 1
6n + 3 + 11 \(⋮\) 2n + 1
3(2n + 1) + 11 \(⋮\) 2n + 1
Ta có 2n + 1 \(⋮\) 2n + 1 nên 3(2n + 1) \(⋮\) 2n + 1
\(\Rightarrow\) 11 \(⋮\) 2n + 1
\(\Rightarrow\) 2n + 1 \(\in\) Ư(11) = {1; -1; 11; -11}
Xét 4 TH:
2n + 1 = 1 \(\Rightarrow\) 2n = 0 \(\Rightarrow\) n = 0 (TM)
2n + 1 = -1 \(\Rightarrow\) 2n = -2 \(\Rightarrow\) n = -1 (TM)
2n + 1 = 11 \(\Rightarrow\) 2n = 10 \(\Rightarrow\) n = 5 (TM)
2n + 1 = -11 \(\Rightarrow\) 2n = -12 \(\Rightarrow\) n = -6 (TM)
Vậy n \(\in\) {0; -1; 5; -6}
Chúc bn học tốt (Dài quá, làm mãi mới hết :v)
CM
12 tháng 7 2018
F(x) là một nguyên hàm của hàm số f(x) => F'(x) = f(x)
Đồng nhất ta được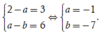 
Chọn B.
CM
1 tháng 6 2019
Đáp án B
Ta có F x = x 2 + a x + b e - x ⇒ F ' x = - x 2 + 2 - a x + a - b e - x
mà f x = F ' x suy ra - x 2 + 2 - a x + a - b = - x 2 + 3 x + 6 ⇒ 2 - a = 3 a - b = 6 ⇔ a = - 1 b = - 7
