Cho tam giác ABC có A ^ = 80 ° , B ^ = 50 ° . Chứng minh tam giác ABC cân.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

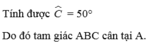

Xét tam giác ABC, có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
=> \(80^o+50^o+\widehat{C}=180^o\)
=> \(\widehat{C}=50^o\)
Ta có:
\(\widehat{B}=50^o\)
\(\widehat{C}=50^o\)
Suy ra: \(\widehat{B}=\widehat{C}\)
=> Tam giác ABC cân tại A.
Góc C bằng :
180o-80o-500=50o
vì Góc C =Góc B nên suy ra Tam giác ABC là tam giác cân

b1 :
DE // AB
=> góc ABC = góc DEC (đồng vị)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> góc DEC = góc ACB
=> tam giác DEC cân tại D (dh)
b2:
a, tam giác ABC => góc A + góc B + góc C = 180 (đl)
góc A = 80; góc B = 50
=> góc C = 50
=> góc B = góc C
=> tam giác ABC cân tại A (dh)
b, DE // BC
=> góc EDA = góc ABC (slt)
góc DEA = góc ECB (dlt)
góc ABC = góc ACB (Câu a)
=> góc EDA = góc DEA
=> tam giác DEA cân tại A (dh)

a: Xét ΔABC vuông tại B và ΔAED vuông tại E có
AC=AD
\(\widehat{A}\) chung
Do đó: ΔABC=ΔAED
b: Đề sai rồi bạn

Bài 1:
Tam giác MNP có: \(\widehat{M}=40^o;\widehat{N}=100^o\)
Tổng số đo 3 góc của 1 tam giác là 180o, ta được:
\(\widehat{M}+\widehat{N}+\widehat{P}=180^o\\ \Leftrightarrow40^o+100^o+\widehat{P}=180^o\\ \Leftrightarrow140^o+\widehat{P}=180^o\\ \Leftrightarrow\widehat{P}=180^o-140^o=40^o\)
Vì: \(\widehat{M}=\widehat{P}=40^o\) => Tam giác MNP là tam giác cân tại N (ĐPCM)

Bn xem lại câu d nhé
`a)`
Có `Delta ABC` cân tại `A`
`=>hat(B)=hat(C)=(180^0-hat(BAC))/2`
hay `hat(B)=hat(C)=(180^0-50^0)/2`
`=>hat(B)=hat(C)=130^0/2=65^0`
`b)`
Có `H` là tđ `BC(GT)=>BH=HC`
Xét `Delta ABH` và `Delta ACH` có :
`{:(AB=AC(GT)),(AH-chung),(BH=CH(cmt)):}}`
`=>Delta ABH=Delta ACH(c.c.c)(đpcm)`
`c)`
Có `AB=AC=>A in` trung trực của `BC`(1)
`BH=CH=>H in` trung trực của `BC`(2)
Từ (1) và (2)`=>AH` là trung trực của `BC`
`=>AH⊥BC(đpcm)`


b2 :
a, xét tam giác ABD và tam giác ACE có: góc A chung
AB = AC do tam giác ABC cân tại A (gt)
góc ADB = góc AEC = 90
=> tam giác ABD = tam giác ACE (ch-cgv)
b, tam giác ABD = tam giác ACE (câu a)
=> góc ABD = góc ACE (đn)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
góc HBC = góc ABC - góc ABD
góc HCB = góc ACB - góc ACE
=> góc HBC = góc HCB
=> tam giác HBC cân tại H (Dh)