Phương trình x 3 - 3 x 2 - m 2 = 0 (với m là tham số thực) có nhiều nhất bao nhiêu nghiệm phân biệt
A. 4 nghiệm.
B. 3 nghiệm.
C. 2 nghiệm.
D. 6 nghiệm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ: ...
\(\Leftrightarrow m^2+m\left(x^2-3x-4\right)-m\sqrt{x+7}-\left(x^2-3x-4\right)\sqrt{x+7}=0\)
\(\Leftrightarrow m\left(x^2-3x-4+m\right)-\sqrt{x+7}\left(x^2-3x-4+m\right)=0\)
\(\Leftrightarrow\left(m-\sqrt{x+7}\right)\left(x^2-3x-4+m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\sqrt{x+7}\left(1\right)\\m=-x^2+3x+4\left(2\right)\end{matrix}\right.\)
Với \(m\) nguyên tố \(\Rightarrow\) (1) luôn có đúng 1 nghiệm
Để pt có số nghiệm nhiều nhất \(\Rightarrow\) (2) có 2 nghiệm pb
\(\Rightarrow y=m\) cắt \(y=-x^2+3x+4\) tại 2 điểm pb thỏa mãn \(x\ge-7\)
\(\Rightarrow-66\le m\le\dfrac{25}{4}\Rightarrow m=\left\{2;3;5\right\}\)

\(\Leftrightarrow\left\{{}\begin{matrix}3.2^xlogx-12logx-2^x+4=0\left(1\right)\\5^x=m\left(2\right)\end{matrix}\right.\) và \(5^x\ge m\) (\(x>0\))
Xét (1):
\(\Leftrightarrow3logx\left(2^x-4\right)-\left(2^x-4\right)=0\)
\(\Leftrightarrow\left(3logx-1\right)\left(2^x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=2\\x_2=\sqrt[3]{10}\end{matrix}\right.\)
\(y=5^x\) đồng biến trên R nên (2) có tối đa 1 nghiệm
Để pt đã cho có đúng 2 nghiệm phân biệt ta có các TH sau:
TH1: (2) vô nghiệm \(\Rightarrow m\le0\) (ko có số nguyên dương nào)
TH2: (2) có nghiệm (khác với 2 nghiệm của (1)), đồng thời giá trị của m khiến cho đúng 1 nghiệm của (1) nằm ngoài miền xác định
(2) có nghiệm \(\Rightarrow m>0\Rightarrow x_3=log_5m\)
Do \(\sqrt[3]{10}>2\) nên bài toán thỏa mãn khi: \(x_1< x_3< x_2\)
\(\Rightarrow2< log_5m< \sqrt[3]{10}\)
\(\Rightarrow25< m< 5^{\sqrt[3]{10}}\) (hơn 32 chút xíu)
\(\Rightarrow\) \(32-26+1\) giá trị nguyên

Chọn đáp án D
Phương pháp
Cho ba số a, b, c lập thành CSN thì ta có: b 2 = a c .
Cách giải
Ta có: ( x - 1 ) ( x - 3 ) ( x - m ) = 0
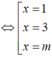
Phương trình đã cho có 3 nghiệm phân biệt
![]()
+) Giả sử 1; 3; m lập thành 1 CSN tăng
![]()
+) Giả sử m; 1; 3 lập thành 1 CSN tăng
![]()
+) Giả sử 1; m; 3 lập thành 1 CSN tăng
![]()
Vậy có 3 giá trị m thỏa mãn

a
Ta có:
\(\Delta'=m^2-\left(2m-3\right)=m^2-2m+3=\left(m-1\right)^2+2>0\)
Nên phương trình luôn có 2 nghiệm phân biệt với mọi m
b
Phương trình có 2 nghiệm trái dấu thì \(2m-3< 0\Leftrightarrow m< \frac{3}{2}\)
Vậy .....................

a)PT có 2 nghiệm phân biệt
`<=>Delta>0`
`<=>(2m+3)^2+4(2m+4)>0`
`<=>4m^2+12m+9+8m+16>0`
`<=>4m^2+20m+25>0`
`<=>(2m+5)^2>0`
`<=>m ne -5/2`
b)Áp dụng vi-ét:
$\begin{cases}x_1+x_2=2m+3\\x_1.x_2=-2m-4\\\end{cases}$
`|x_1|+|x_2|=5`
`<=>x_1^2+x_2^2+2|x_1.x_2|=25`
`<=>(x_1+x_2)^2+2(|x_1.x_2|-x_1.x_2)=25`
`<=>(2m+3)^2+2[|-2m-4|-(-2m-4)]=25`
Với `-2m-4>=0<=>m<=-2`
`=>pt<=>(2m+3)^2-25=0`
`<=>(2m-2)(2m+8)=0`
`<=>(m-1)(m+4)=0`
`<=>` $\left[ \begin{array}{l}x=1\\x=-4\end{array} \right.$
`-2m-4<=0=>m>=-2=>|-2m-4|=2m+4`
`<=>4m^2+12m+9+8m+16=25`
`<=>4m^2+20m=0`
`<=>m^2+5m=0`
`<=>` \left[ \begin{array}{l}x=0\\x=-5\end{array} \right.$
Vậy `m in {0,1,-4,-5}`

\(x-4\sqrt{x+3}+m=0\)
\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)
\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)
\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)
\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)
\(\Rightarrow f\left(0\right)=-3\)
\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)
\(t^2-4t-3+m=0\Leftrightarrow t^2-4t-3=-m\)
\(có-2nghiệm-pb-trên[0;\text{+∞})\)
\(xét-bảng-biến-thiên-củaf\left(t\right)=t^2-4t-3,trên[0;\text{+∞})\)
dựa vào bảng biến thiên ta thấy số nghiệm của phương trình f(t)
là số giao điểm của đường thẳng y=-m
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)
Đáp án B
Phương pháp:
Số nghiệm của phương trình |x3| - 3x2 - m2 = 0 bằng số giao điểm của đồ thị hàm số y = |x|3 - 3x2 và đường thẳng y = m2
Phác họa đồ thị hàm số , từ đó nhận xét số giao điểm trên.
Cách giải:
Số nghiệm của phương trình |x3| - 3x2 - m2 = 0 bằng số giao điểm của đồ thị hàm số y = |x|3 - 3x2 và đường thẳng y = m2
Từ đồ thị hàm số y = x3 - 3x2
Ta vẽ được đồ thị hàm số y = |x|3 - 3x2 như sau:
Do m2 ≥ 0,∀m nên đồ thị hàm số y = |x|3 - 3x2 cắt đường thẳng y = m2 tại nhiều nhất 3 điểm.