Cho các hàm số
y
=
log
a
x
,
y
=
log
b
x
v
à
y
=
c
x
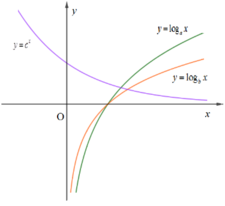
(với a, b, c là các số dương khác 1) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng? A. c > b > a B. c > a > b C. a > b > c D. b > a >...
Đọc tiếp
Cho các hàm số y = log a x , y = log b x v à y = c x (với a, b, c là các số dương khác 1) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A. c > b > a
B. c > a > b
C. a > b > c
D. b > a > c
Đáp án D
Cách giải:
Ta thấy, hai hàm số y = logax, y = logbx đều đồng biến trên (0;+∞) ⇒ a, b > 1
Lấy x0 > 0 bất kì, ta thấy logax0 > logbx0 ⇒ a < b ⇒ 1 < a < b
Hàm số y = cx nghịch biến trên R ⇒ c < 1 ⇒ c < a < b