Cho tam giác ABC các đg` cao AD,BE,CF cắt nhau tại H.
CM HD+HE+HF<=3r. (r là bk đtnt tam giác ABC).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CP
0
Những câu hỏi liên quan
đó nha bn3 tháng 5 2021
a,Xét tg DHB và tg DCA có: ^HDB=^CDA=90 độ, ^DBH=^DAC ( cùng phụ với hai góc bằng nhau BHD=^AHE)
Do đó: tg HDB đồng dạng tg DCA (g.g)
Suy ra: HD/DC=BD/DA-> bd*dc=dh*da
b, HD/HA=SBHC/SABC
HE/BE=SAHC/SABC
HF/CF=SHAB/SABC
HD/HA+HE/BE+HF/CF=SBHC/SABC+SAHC/SABC+SAHB/SABC=1
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
Đây là 1 trường hợp của BĐT hình học quan trọng: BĐT Erdos-Mordell
Cách chứng minh bài này y hệt như cách người ta chứng minh BĐT nói trên.
Có khoảng gần 20 cách gì đó, em kiếm trên google thử coi, vì BĐT này quá quen thuộc rồi nên mình sẽ ko chứng minh lại ở đây.
HH
15 tháng 4 2020
Hơi khó nên tui dung tạm BĐT vậy , bạn thông cảm ^ ^
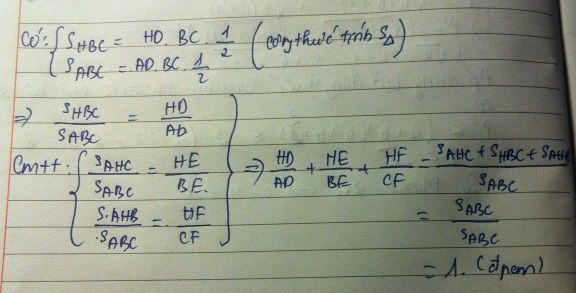
\(S\left(ABC\right)=AD.\frac{BC}{2}\)
\(S\left(BHC\right)=HD.\frac{BC}{2}\)
\(\Rightarrow\frac{HD}{AD}=\frac{S\left(BHC\right)}{S\left(ABC\right)}\left(1\right)\)
Tương tự:
\(\frac{HE}{BE}=\frac{S\left(AHC\right)}{S\left(ABC\right)}\left(2\right)\)
\(\frac{HF}{CF}=\frac{S\left(AHB\right)}{S\left(ABC\right)}\left(3\right)\)
(1) + (2) +(3) được:
\(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\left[S\left(BHC\right)+S\left(AHC\right)+\frac{S\left(AHB\right)}{S\left(ABC\right)}\right]=\frac{S\left(ABC\right)}{S\left(ABC\right)}=1\)
Áp dụng bất đẳng thức: \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)9 ta có:
\(\left(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}\right)\left(\frac{AD}{HD}+\frac{BE}{HE}+\frac{CF}{HF}\right)\ge9\)
mà: \(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=1\) \(\Rightarrow\left(\frac{AD}{HD}+\frac{BE}{HE}+\frac{CF}{HF}\right)\ge9\)
HC
30 tháng 6 2019
Ad ĐỪNG XÓA
Học tiếng anh free vừa học vừa chơi đây
các bạn vào đây đăng kí nhá : https://iostudy.net/ref/165698