Tính nhanh: A = 1 1.2 + 1 2.3 + ... + 1 2017.2018
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
15 tháng 1 2018
Đúng(0)
Những câu hỏi liên quan
L
0
L
2
8 tháng 4 2018
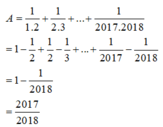
Ta có :
\(A=\frac{1+\left(1+2\right)+\left(1+2+3\right)+...+\left(1+2+3+...+2017\right)}{1.2+2.3+3.4+...+2017.2018}\)
\(A=\frac{\frac{2}{2}+\frac{2\left(2+1\right)}{2}+\frac{3\left(3+1\right)}{2}+...+\frac{2017\left(2017+1\right)}{2}}{1.2+2.3+3.4+...+2017.2018}\)
\(A=\frac{\frac{2}{2}+\frac{2.3}{2}+\frac{3.4}{2}+...+\frac{2017.2018}{2}}{1.2+2.3+3.4+...+2017.2018}\)
\(A=\frac{\frac{1.2+2.3+3.4+...+2017.2018}{2}}{1.2+2.3+3.4+...+2017.2018}\)
\(A=\frac{1.2+2.3+3.4+...+2017.2018}{2}.\frac{1}{1.2+2.3+3.4+...+2017.2018}\)
\(A=\frac{1}{2}\)
Vậy \(A=\frac{1}{2}\)
Chúc bạn học tốt ~
TN
3
21 tháng 2 2023
Trước tiên, chúng ta cần có lý thuyết về biến đổi phân số.
\(\dfrac{b-a}{a\cdot b}=\dfrac{1}{a}-\dfrac{1}{b}\)
Ta có:
\(S=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2017\cdot2018}\)
\(S=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2017}-\dfrac{1}{2018}\)
\(S=1+\left(-\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+...-\dfrac{1}{2018}\)
\(S=1-\dfrac{1}{2018}\)
\(S=\dfrac{2017}{2018}\)
21 tháng 2 2023
=1/1.2+1/2.3+1/3.4+...1/2017.2018
=1/1-1/2+1/2-1/3+1/3-1/4+...+1/2017-1/2018
=1-1/2018
=2018/2018-1/2018
=2017/2018
HN
1
8 tháng 7 2019
A = 1.2 + 2.3 + 3.4 + ....... + 99.100
3A = 1.2.3 + 2.3.3 + 3.4.3 + ....... + 99 . 100 . 3
3A = 1.2.3 + 2.3.(4-1) + 3.4.(5-2) +.... + 99.100.(101-98)
3A = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ..... + 99 . 100 . 101 - 98 . 99 . 100
3A = (1.2.3 - 1.2.3) + (2.3.4-2.3.4) + ... + (98.99.100 - 98.99.100) + 99 . 100 . 101
3A = 99 . 100 . 101 = 999900
A = 999900 : 3
A = 333300
P
18 tháng 3 2018
1. 3S= 1.2.(3-0)+ 2.3.(4-1)+...+ n.(n+1).[(n+2)-(n-1)]
=[1.2.3+ 2.3.4+...+ (n-1)n(n+1)+ n(n+1)(n+2)]- [0.1.2+ 1.2.3+...+(n-1)n(n+1)]
=n(n+1)(n+2)
=>S
Biểu thức này dùng để tính tổng 1^2+..+n^2 rất tiện và thực tế cũng là ket quả của hệ quả trên.
dùng cách thức tương tự có thể tính S=1.2.3+...+ n(n+1)(n+2) từ đó suy ra tổng 1^3+...+n^3
Việc sử dụng trước kết quả tổng 1^2+...+n^2 theo tôi là ngược tiến trình.
2. S = 1.2.3 + 2.3.4 +..+ (n-1).n.(n+1)
4S = 1.2.3.4 + 2.3.4.4 + 3.4.5.4 +..+ (n-1)n(n+1).4
ghi dọc cho dễ nhìn:
(k-1)k(k+1).4 = (k-1)k(k+1)[(k+2) - (k-2)] = (k-1)k(k+1)(k+2) - (k-2)(k-1)k(k+1)
ad cho k chạy từ 2 đến n ta có:
1.2.3.4 = 1.2.3.4
2.3.4.4 = 2.3.4.5 - 1.2.3.4
3.4.5.4 = 3.4.5.6 - 2.3.4.5
...
(n-2)(n-1)n.4 = (n-2)(n-1)n(n+1) - (n-3)(n-2)(n-1)n
(n-1)n(n+1).4 = (n-1)n(n+1)(n+2) - (n-2)(n-1)n(n+1)
+ + cộng lại vế theo vế + + (chú ý cơ chế rút gọn)
4S = (n-1)n(n+1)(n+2)
3.
S
4 tháng 5 2023
\(A=2017:\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2017.2018}\right)\)
\(=2017:\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2017}-\dfrac{1}{2018}\right)\)
\(=2017:\left(1-\dfrac{1}{2018}\right)\)
\(=2017:\dfrac{2017}{2018}\)
\(=2017\cdot\dfrac{2018}{2017}\)
\(=2018\)
#NgDat
NK
4 tháng 5 2023
\(A=2017:\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2017\cdot2018}\right)\)
\(A=2017:\left(\dfrac{1}{1}\cdot\dfrac{1}{2}+\dfrac{1}{2}\cdot\dfrac{1}{3}+\dfrac{1}{3}\cdot\dfrac{1}{4}+...+\dfrac{1}{2017}\cdot\dfrac{1}{2018}\right)\)
\(A=2017:\left(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2017}-\dfrac{1}{2018}\right)\)
\(A=2017:\left(\dfrac{1}{1}-\dfrac{1}{2018}\right)\)
\(A=2017:\left(\dfrac{2018}{2018}-\dfrac{1}{2018}\right)\)
\(A=2017:\dfrac{2017}{2018}\)
\(A=2018.\)
31 tháng 12 2017
\(\frac{1}{1.2}\)\(+\frac{1}{2.3}+\)\(\frac{1}{3.4}\)\(+\)\(.............+\)\(\frac{1}{2017.2018}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+......+\frac{1}{2017}-\frac{1}{2018}\)
\(=\frac{1}{1}-\frac{1}{2018}\)
\(=\frac{2017}{2018}\)
31 tháng 12 2017
\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+.........+\frac{1}{2017.2018}\)
\(=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+......+\frac{2018-2017}{2017.2018}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+......+\frac{1}{2017}-\frac{1}{2018}\)
\(=1-\frac{1}{2018}\)
\(=\frac{2017}{2018}\)
NT
0
LT
4
5 tháng 4 2018
\(S=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2017.2018}+\frac{1}{2018.2019}\)
\(S=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2017}-\frac{1}{2018}+\frac{1}{2018}-\frac{1}{2019}\)
( gạch bỏ các phân số giống nhau)
\(S=1-\frac{1}{2019}\)
\(S=\frac{2018}{2019}\)
CHÚC BN HỌC TỐT!!!!
MT
5 tháng 4 2018
S=1/1.2+1/2.3+1/3.4+............1/2017.2018+1/2018.2019
S=1/2.(1+1/3.2+1/3.2+.............1/2017.1009+1/1009.2019)
S=1/4.(2+2/3.2+2/3.2+..............2/2017.1009+2/1009.2019)
S=1/4.(1-1/2+1/2-1/3+1/3+..........+1/1009-1/1009+1/2019)
S=1/4.(1-1/2019)
S=1/4.2018/2019=1009/4038
DJ
1
21 tháng 12 2017
D=1.2+2.3+3.4+...+2017.2018
=>3D=1.2.3+2.3.3+3.4.3+...+2017.2018.3
=>3D=1.2.(3-0)+2.3.(4-1)+3.4.(5-2)+...+2017.2018.(2019-2016)
=>3D=1.2.3-0.1.2+2.3.4-1.2.3+3.4.5-2.3.4+...+2017.2018.2019-2016.2017.2018
=>3D=2017.2018.2019/3
=>D=2739315938
k mk nha $_$
:D