Tính: B = 3 1.3 + 3 3.5 + 3 5.7 + ... + 3 199.201
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 3 2018
Đúng(0)
Những câu hỏi liên quan
PT
4
NH
17 tháng 6 2019
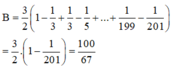
\(D=\frac{3}{1.3}+\frac{3}{3.5}+...+\frac{3}{199.201}\)
\(D=\frac{3}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+...+\frac{2}{199.201}\right)\)
\(D=\frac{3}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{199}-\frac{1}{201}\right)\)
\(D=\frac{3}{2}\left(1-\frac{1}{201}\right)\)
\(D=\frac{3}{2}.\frac{200}{201}\)
\(D=\frac{100}{67}\)
T
17 tháng 6 2019
#)Giải :
\(D=\frac{3}{1.3}+\frac{3}{3.5}+\frac{3}{5.7}+...+\frac{3}{199.201}\)
\(D=\frac{3}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{199.201}\right)\)
\(D=\frac{3}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{199}-\frac{1}{201}\right)\)
\(D=\frac{3}{2}\left(1-\frac{1}{201}\right)\)
\(D=\frac{3}{2}\times\frac{200}{201}\)
\(D=\frac{100}{67}\)
TY
3 tháng 3 2017
\(A=\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{199.201}\).
\(2A=\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{199.201}\)
\(2A=\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{199}-\frac{1}{201}\)
\(2A=\frac{1}{1}-\frac{1}{201}\)
\(2A=\frac{201-1}{201}\)
\(2A=\frac{200}{201}\)
\(A=\frac{200}{201}:2\)
\(A=\frac{200}{402}\)
18 tháng 3 2017
G=7/2.(2/1.3+2/3.5+2/5.7+...+2/199.201)
G=7/2.(1-1/3+1/3-1/5+1/5-1/7+.....+1/199.201
G=7/2.(1-1/201)
G=7/2.200/201
G=1400/402
G=700/201
TM
18 tháng 3 2017
\(G=\frac{7}{1.3}+\frac{7}{3.5}+\frac{7}{5.7}+...+\frac{7}{199.201}\)
\(G=7\left(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{199.200}\right)\)
\(G=\frac{7}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{199.201}\right)\)
\(G=\frac{7}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{199}-\frac{1}{201}\right)\)
\(G=\frac{7}{2}\left(1-\frac{1}{201}\right)\)
\(G=\frac{7}{2}.\frac{200}{201}\)
\(G=\frac{700}{201}\)
DT
5
15 tháng 4 2016
3.2/1.3.2+3.2/3.5.2+3.2/5.7.2+...+3.2/49.51
3/2(2/1.3+2/3.5+2/5.7+....+2/49.51)
3/2(1-1/3+1/3-1/5+1/5-1/7+....+1/49-1/51)
3/2(1-1/51)
3/2 . 50/51
25/17
15 tháng 4 2016
áp dụng công thức nếu có thừa số thứ 2 ở mẫu trừ đi thừa số thứ 1 bằng số trên tử thi \(\frac{1}{a}-\frac{1}{b}\) ab ở đây là 2 thừa số ở mẫu
VD;3/1.3+3/3.5+...+3/49.51(vì tất cả mẫu trừ cho nhau đều =tử)
nên = 1/1-1/3+1/3+1/5+...+1/49-1/51
=1-1/51
=50/51
NT
2
11 tháng 4 2015
=3.(3/1.3+3/3.5+3/5.7+...+3/95.97+3/97.99)
=3(1-1/3+1/3-1/5+1/5-1/7+...+1/95-1/97+1/97-1/99)
=3[(1-1/99)+(1/5-1/5)+(1/7-1/7)+...+(1/97-1/97)]
=3(1-1/99)=3(99/99-1/99)=3.98/99=1.98/33=98/33
NM
0
NT
1
10 tháng 11 2016
em gửi bài qua fb của thầy thầy HD nhé: tìm fb của thầy bằng sđt:0975705122 nhé