Đặt và Hãy biểu diễn theo m và n.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Ta có
log 6125 7 = log 6125 + log 7 = log 7 2 . 125 + 1 2 log 7
= 5 2 log 7 + log 5 3 = 5 2 n + 3 log 5 = 5 2 n + 3 1 - log 2
= 5 2 n + 3 - 3 m .

a: \(log_2\left(mn\right)=log_2\left(2^7\cdot2^3\right)=7+3=10\)
\(log_2m+log_2n=log_22^7+log_22^3=7+3=10\)
=>\(log_2\left(mn\right)=log_2m+log_2n\)
b: \(log_2\left(\dfrac{m}{n}\right)=log_2\left(\dfrac{2^7}{2^3}\right)=7-3=4\)
\(log_2m-log_2n=log_22^7-log_22^3=7-3=4\)
=>\(log_2\left(\dfrac{m}{n}\right)=log_2m-log_2n\)
a) \(\log_2\left(mn\right)=\log_2\left(2^7.2^3\right)=\log_22^{7+3}=\log_22^{10}=10.\log_22=10.1=10\)
\(\log_2m+\log_2n=\log_22^7+\log_22^3=7\log_22+3\log_22=7.1+3.1=7+3=10\)
b) \(\log_2\left(\dfrac{m}{n}\right)=\log_2\dfrac{2^7}{2^3}=\log_22^4=4.\log_22=4.1=4\)
\(\log_2m-\log_2n=\log_22^7-\log_22^3=7.\log_22-3\log_22=7.1-3.1=4\)

\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)

a: \(log_49=\dfrac{log9}{log4}=\dfrac{log3^2}{log2^2}=\dfrac{2\cdot log3}{2\cdot log2}=\dfrac{log3}{log2}=\dfrac{b}{a}\)
b: \(log_612=\dfrac{log12}{log6}=\dfrac{log2^2+log3}{log2+log3}=\dfrac{2\cdot log2+log3}{log2+log3}\)
\(=\dfrac{2a+b}{a+b}\)
c: \(log_56=\dfrac{log6}{log5}=\dfrac{log\left(2\cdot3\right)}{log\left(\dfrac{10}{2}\right)}=\dfrac{log2+log3}{log10-log2}\)
\(=\dfrac{a+b}{1-a}\)
a: l o g 4 9 = l o g 9 l o g 4 = l o g 3 2 l o g 2 2 = 2 ⋅ l o g 3 2 ⋅ l o g 2 = l o g 3 l o g 2 = b a log 4 9= log4 log9 = log2 2 log3 2 = 2⋅log2 2⋅log3 = log2 log3 = a b b: l o g 6 12 = l o g 12 l o g 6 = l o g 2 2 + l o g 3 l o g 2 + l o g 3 = 2 ⋅ l o g 2 + l o g 3 l o g 2 + l o g 3 log 6 12= log6 log12 = log2+log3 log2 2 +log3 = log2+log3 2⋅log2+log3 = 2 a + b a + b = a+b 2a+b c: l o g 5 6 = l o g 6 l o g 5 = l o g ( 2 ⋅ 3 ) l o g ( 10 2 ) = l o g 2 + l o g 3 l o g 10 − l o g 2 log 5 6= log5 log6 = log( 2 10 ) log(2⋅3) = log10−log2 log2+log3 = a + b 1 − a = 1−a a+b

\(log_{12}21=\dfrac{log_321}{log_312}=\dfrac{log_3\left(7\cdot3\right)}{log_3\left(2^2\cdot3\right)}=\dfrac{log_37+log_33}{log_34+log_33}\)
\(=\dfrac{log_37+1}{log_32^2+1}=\dfrac{log_37+1}{2\cdot log_32+1}=\dfrac{b+1}{2a+1}\)


a: \(log_2\left(M\cdot N\right)=log_2\left(2^5\cdot2^3\right)=log_2\left(2^8\right)=8\)
\(log_2M+log_2N=log_22^5+log_22^3=5+3=8\)
=>\(log_2\left(MN\right)=log_2M+log_2N\)
b: \(log_2\left(\dfrac{M}{N}\right)=log_2\left(\dfrac{2^5}{2^3}\right)=log_2\left(2^2\right)=2\)
\(log_2M-log_2N=log_22^5-log_22^3=5-3=2\)
=>\(log_2\left(\dfrac{M}{N}\right)=log_2M-log_2N\)

a) \(y = {\log _a}M \Leftrightarrow M = {a^y}\)
b) Lấy loogarit theo cơ số b cả hai vế của \(M = {a^y}\) ta được
\({\log _b}M = {\log _b}{a^y} \Leftrightarrow {\log _b}M = y{\log _b}a \Leftrightarrow y = \frac{{{{\log }_b}M}}{{{{\log }_b}a}}\)

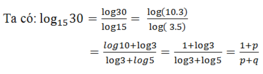
Đáp án D.
Ta có:
log 6125 7 = log 6125 + log 7 = log 7 2 .125 + 1 2 log 7 = 2 log 7 + log 125 + 1 2 log 7 = 5 2 log 7 + log 5 3 = 5 2 n + 3 log 5 = 5 2 n + 3 1 − log 2 = 5 2 n + 3 − 3 m .