Question

[Pham Trong Bach]

Cho tứ diện ABCD có A D ⊥ ( A B C ) , đáy ABC thỏa mãn điều kiện:

cot A + cot B + cot C 2 = B C A B . A C + C A B A . B C + A B C A . C B .

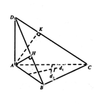
Gọi H, K lần lượt là hình chiếu vuông góc của A lên BD và BC. Tính thể tích V của khối cầu ngoại tiếp khói chóp A.BCHK

A. V = 4 π 3 .

B. V = 32 π 3 .

C. V = 8 π 3 .

D. V = 4 π 3 3 .

Answer 1

[Cao Minh Tâm]

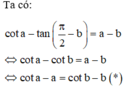
Đáp án B.

*Xác định tâm mặt cầu ngoại tiếp hình chóp A.BCHK

Gọi E, F lần lượt là trung điểm của AC và AB. Trong mặt phẳng (ABC), kẻ các đường thẳng d, d’ lần lượt vuông góc với AC và AB tại E, F. Do D A ⊥ d , D A ⊥ d '  (do D A ⊥ A B C ) nên d ⊥ D A C , d ' ⊥ D A B .  Gọi I là giao điểm của d, d’ thì I chính là tâm của mặt cầu chứa hai đường tròn ngoại tiếp hai tam giác AHC, AKC. Hay nói cách khác, I là tâm mặt cầu ngoại tiếp hình chóp A.BCHK, bán kính R = IA cũng chính là bán kính đường tròn ngoại tiếp  Δ A B C  (do IA = IB = IC).

*Một số hệ thức cần nhớ trong tam giác

Cho Δ A B C ,  gọi AH là đường cao  H ∈ B C .  R, r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp tam giac, p là nửa chu vi. Kí hiệu BC = a, AC = b, AB = c, diện tích S Δ A B C = S .  

1. Định lý cosin:

  a 2 = b 2 + c 2 − 2 b c cos A ; b 2 = a 2 + c 2 − 2 a c cos B ; c 2 = a 2 + b 2 − 2 a b cos C .

2. Định lý sin: a sin A = b sin B = c sin C = 2 R .  

3. Độ dài trung tuyến xuất phát từ các đỉnh A, B, C (Kí hiệu lần lượt là m a , m b , m c ):

m a 2 = b 2 + c 2 2 − a 2 4 ; m b 2 = a 2 + c 2 2 − b 2 4 ; m c 2 = a 2 + b 2 2 − c 2 4 .

4. Các công thức tính diện tích tam giác:

S = 1 2 a . h a = 1 2 b . h b = 1 2 c . h c S = 1 2 b c sin A = 1 2 a c sin B = 1 2 a b sin C S = a b c 4 R = p r = p p − a p − b p − c .

5. Định lý tang:

  a − b a + b = tan A − B 2 tan A + B 2 ; b − c b + c = tan B − C 2 tan B + C 2 ; c − a c + a = tan C − A 2 tan C + A 2 .

6. Định lý cotang:  

cot A = b 2 + c 2 − a 2 4 S ; cot B = a 2 + c 2 − b 2 4 S ; cot C = a 2 + b 2 − c 2 4 S . → cot A + cot B + cot C = a 2 + b 2 + c 2 4 S .

*Phân tích dữ kiện đề bài:

  cot A + cot B + cot C 2 = B C A B . A C + C A B A . B C + A B C A . C B ⇔ A B 2 + B C 2 + C A 2 8 S Δ A B C = B C 2 + C A 2 + A B 2 A B . A C . B C ⇔ 8 S Δ A B C = A B . A C . B C ⇔ 8. A B . A C . B C 4 R = A B . A C . B C ⇔ R = 2 = I A .

Vậy thể tích mặt cầu ngoại tiếp hình chóp A.BCHK là:

V = 4 3 π R 3 = 4 3 π 2 3 = 32 π 3  (đvtt).