Cho hàm số f(x) có f ( 1 ) = 1, f ( m + n ) = f ( m ) + f ( n ) + m n , ∀ m , n ∈ ℕ * . Giá trị của biểu thức T = log f ( 96 ) − f ( 69 ) − 241 2 là
A.4
B.3
C.6
D.9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
0
HP
27 tháng 1 2021
\(f\left(20\right)=f\left(1\right)+f\left(19\right)+3\left(4.1.19-1\right)=f\left(19\right)+12.19-3\)
\(f\left(19\right)=f\left(18\right)+12.18-3\)
\(f\left(18\right)=f\left(17\right)+12.17-3\)
.....
\(f\left(3\right)=f\left(2\right)+12.2-3\)
\(f\left(2\right)=f\left(1\right)+12-3\)
Cộng vế theo vế các đẳng thức trên:
\(f\left(2\right)+f\left(3\right)+...+f\left(20\right)=f\left(1\right)+f\left(2\right)+...+f\left(19\right)+12\left(1+2+...+19\right)-3.20\)
\(\Leftrightarrow f\left(20\right)=2220\)
Đoạn này bạn tính kĩ một chút nha, mình tính không biết có sai không.
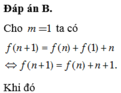
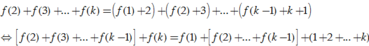
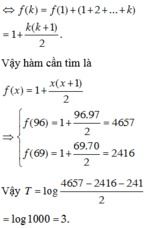
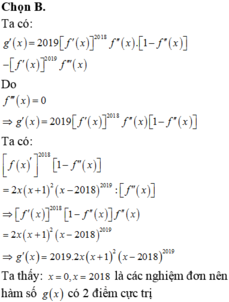
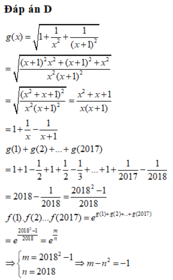
Đáp án B.
Cho m=1 ta có
f ( n + 1 ) = f ( n ) + f ( 1 ) + n ⇔ f ( n + 1 ) = f ( n ) + n + 1.
Khi đó
f ( 2 ) + f ( 3 ) + ... + f ( k ) = f ( 1 ) + 2 + f ( 2 ) + 3 + ... + f ( k − 1 ) + k + 1
⇔ f ( 2 ) + f ( 3 ) + ... + f ( k − 1 ) + f ( k ) = f ( 1 ) + f ( 2 ) + ... + f ( k − 1 ) + ( 1 + 2 + ... + k )
⇔ f ( k ) = f ( 1 ) + ( 1 + 2 + ... + k ) = 1 + k ( k + 1 ) 2 .
Vậy hàm cần tìm là
f ( x ) = 1 + x ( x + 1 ) 2 ⇒ f ( 96 ) = 1 + 96.97 2 = 4657 f ( 69 ) = 1 + 69.70 2 = 2416
Vậy
T = log 4657 − 2416 − 241 2 = log 1000 = 3.