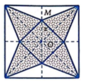
Cắt một miếng giấy hình vuông và xếp thành một hình chóp tứ giác đều (hình vẽ). Biết cạnh hình vuông bằng 20 (cm), OM = x (cm). Tìm x để hình chóp đều ấy có thể tích lớn nhất.
A. x = 9 (cm)
B. x = 8 (cm)
C. x = 6 (cm)
D. x = 7 (cm)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 7 2019
Đáp án C
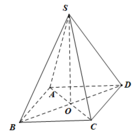
S A = 1 − x 2 2 2 + 1 4 = 1 − x 2 + x 2 2 A O = x 2 2 , S O = S A 2 − A O 2 = 1 − x 2 + x 2 − x 2 2 = 1 − x 2 2 V = 1 3 S O . S A B C D = 1 3 x 2 1 − x 2 2 f ( x ) = x 2 1 − x 2 2 , x ∈ 0 ; 1 f ' ( x ) = 4 x − 5 2 x 2 4 1 − x 2 2 f ' ( x ) = 0 ⇔ x = 0 ( L ) x = 2 2 5
'
CM
15 tháng 4 2018
Đáp án là C
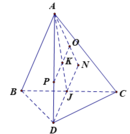
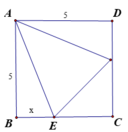
Hình chóp tạo thành có đáy là hình vuông diện tích
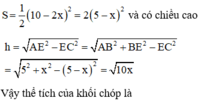
Đáp án B.
Sau khi cắt miếng giấy hình vuông như hình vẽ, ta xếp lại được thành hình chóp tứ giác đều S.MNPQ (hình bên).
Gọi H là trung điểm P Q ⇒ O H = M N 2 = 2 x 2 (cm) và S H = 10 2 - 2 x 2 (cm).
Suy ra S O = S H 2 - O H 2 = 10 2 - 2 x 2 2 - 2 x 2 2 = 20 ( 10 - x ) .
Thể tích khối chóp S.MNPQ là:
V M N P Q = 1 3 . S O . S M N P Q = 1 3 20 ( 10 - x ) . 2 x 2 = 20 3 ( 40 - 4 x ) . x 4
→ V M N P Q = 20 3 ( 40 - 4 x ) . x . x . x . x ≤ 20 3 40 - 4 x + x + x + x + x 5 = 256 10 3
Dấu “=” xảy ra ⇔ 40 - 4 x = x ⇔ x = 8 (cm).