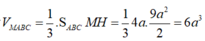Cho lăng trụ đứng ABC.A’B’C’ có AB = AC = a, B C = a 3 . Cạnh bên AA' = 2a. Bán kính mặt cầu ngoại tiếp tứ diện AB’C’C bằng
A. a
B. a 5
C. a 3
D. a 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


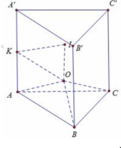

Gọi H là trung điểm của BC.
Ta có tam giác ABC đều nên AH⊥ (BCD) , mà (ABC) ⊥ (BCD) → AH ⊥ (BCD).
Ta có AH⊥ HD→AH = AD.tan600 =a3√ & HD = AD.cot600 =a3√3
ΔBCD→BC = 2HD = 2a3√3suy ra V=13SBCD.AH=13.12BC.HD.AH=a33√9
Gọi H là trung điểm của BC.
Ta có tam giác ABC đều nên AH⊥ (BCD) , mà (ABC) ⊥ (BCD) → AH ⊥ (BCD).
Ta có AH⊥ HD→AH = AD.tan600 =a3√ & HD = AD.cot600 =a3√3
ΔBCD→BC = 2HD = 2a3√3suy ra V=13SBCD.AH=13.12BC.HD.AH=a33√9
Gọi H là trung điểm của BC.
Ta có tam giác ABC đều nên AH⊥ (BCD) , mà (ABC) ⊥ (BCD) → AH ⊥ (BCD).
Ta có AH⊥ HD→AH = AD.tan600 =a3√ & HD = AD.cot600 =a3√3
ΔBCD→BC = 2HD = 2a3√3suy ra V=13SBCD.AH=13.12BC.HD.AH=a33√9

Đáp án là D
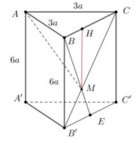
Kẻ MH vuông góc với BC ta có MH ⊥ (ABC) .
Theo định lý Talet
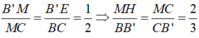
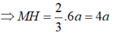
Tam giác ABC vuông cân tại A nên
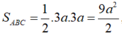
vậy