Cho hình chóp S.ABC có AB = 2a, AC = 4a, BC = 3a. Gọi H là hình chiếu của S nằm trong tam giác ABC. Các mặt bên tạo với đáy một góc 45 ° . Tính thể tích khối chóp S.ABC.
A. V = 15 a 3 6 .
B. V = 3 15 a 3 4 .
C. V = 15 a 3 8 .
D. V = 5 a 3 8 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
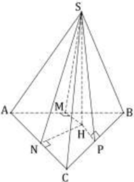
Theo giả thiết, các mặt bên tạo với đáy một góc 45 độ nên hình chiếu vuông góc của S trên (ABC) chính là tâm đường tròn nội tiếp tam giác ABC hay H là tâm đường tròn nội tiếp tam giác ABC.


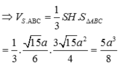

Đáp án D
Ta có S H ⊥ A B C ⇒ S B ; A B C ^ = S B ; B C ^ = S B C ^ = 60 °
Tam giác SBH vuông tại H, có S H = tan 60 ° . B H = a 3
Và S A B C = 1 2 . A B . A C = a 2 3 2 .
Vậy thể tích khối chóp là V S . A B C D = 1 3 . S H . S A B C = 1 3 a 3 a 2 3 2 = a 3 2

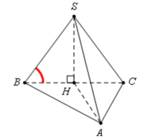
Gọi O là trung điểm của AB![]()
Ta có 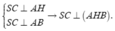
![]()
Trong tam giác vuông SOC có 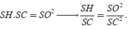
Ta có 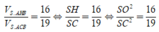
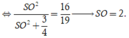
Vậy ![]()
Chọn C.
Đáp án D
Theo giả thiết, các mặt bên tạo với đáy một góc 45 ° nên hình chiếu vuông góc của S trên (ABC) chính là tâm đường tròn nội tiếp ΔABC hay H là tâm đường tròn nội tiếp ΔABC .
Áp dụng công thức Hê-rông em tính được p = 9 a 2 và S ΔABC = 3 15 a 2 4 .
Em lại có: S ΔABC = p . r với r là bán kính đường tròn nội tiếp tam giác ABC.
Từ H, em kẻ HM, HN, HP lần lượt vuông góc với AB, AC, BC thì
=> Góc giữa (SAC) và (ABC) chính là góc giữa SN và HN hay SNH ⏜ = 45 °