Cho hàm số y = ax 3 + bx 2 + cx + d có đồ thị như hình bên
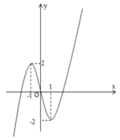
Chọn đáp án ĐÚNG?
A. Hàm số có hệ số a < 0.
B. Hàm số đồng biến trên các khoảng (-2;-1) và (1;2).
C. Hàm số không có cực trị.
D. Hệ số tự do của hàm số khác 0.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Đồ thị hàm số y = a x , y = b x là đồ thị của hàm số mũ cơ bản đồng biến nên a > 1; b > 1
Dựa vào đồ thị ta có :
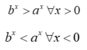
Do đó: b > a > 1
Đồ thị hàm số y = c x là đồ thị của hàm số mũ cơ bản nghịch biến nên 0 < c < 1
Vậy b > a > c

Chọn D.
Dựa vào đồ thị, ta có tiệm cận đứng x = 1, tiệm cận ngang y = 2 và đồ thị đi qua điểm (0; 1) nên
![]()
![]()
Đồ thị hàm số y = a x - 1 b x + c có tiệm cận đứng x = 1 b , tiệm cân ngang y = a b 2
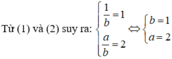

Chọn D.
Dựa vào đồ thị, ta có tiệm cận đứng x = 1 , tiệm cận ngang y = 2 và đồ thị đi qua điểm 0 ; 1 (1). Đồ thị hàm số y = a x - 1 b x + c có tiệm cận đứng x = - c b , tiệm cận ngang y = a và đi qua điểm 0 ; - 1 b (2). Từ (1) và (2) suy ra: a = 2 , b = 1 , c = - 1 .

Chọn B.
Dựa vào đồ thị, ta có tiệm cận đứng x = - 1 , tiệm cận ngang y = 1 1
Đồ thị hàm số y = a x - 1 x + b có tiệm cận đứng x = - b , tiệm cận ngang y = a 2
Từ (1) và (2) suy ra: a = 1 , b = 1 .

Đồ thị hàm số có tiệm cận đứng x = a > 0; tiệm cận ngang y = b > 0
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên
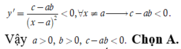

c: Thay x=1 và y=1 vào hàm số, ta được:
y=2x1-3=-1<>1
Vậy: Điểm M ko thuộc đồ thị
b: Hàm số đồng biến vì a=2>0

Ta vẽ đường thẳng x = 1 cắt các đồ thi hàm số đã cho tại tung độ lần lượt a; b; c
Vậy a < b < c. Chọn B
Đáp án B