Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(0;2;0), Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 điểm trong 5 điểm O, A, B, C, D?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có xA' = 2xO-xA = 3; yA' = 2yO-yA = -2; zA' = 2zO-zA=1. Vậy A'(3;-2;1).

Đáp án B
Phương pháp :
A
(
2
;
1
;
-
1
)
,
B
(
3
;
3
;
1
)
,
C
(
4
;
5
;
3
)
.
![]()
=> A, B, C thẳng hàng.

Chọn B.
Gọi B, C, D lần lượt là hình chiếu của A lên các trục Ox , Oy , Oz ⇒ B ( 1 ; 0 ; 0 ) C ( 0 ; - 1 ; 0 ) D ( 0 ; 0 ; 2 )
Suy ra phương trình mặt phẳng ( Q ) : x 1 + y - 1 + z 2 = 1 ⇔ 2 x - y + z - 2 = 0 .

Chọn C.
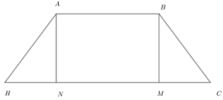
Phương pháp: Sử dụng các véc tơ bằng nhau.

Giả sử M,N lần lượt là hình chiếu của A, B lên CH.



Đáp án B
A B → ( − 1 ; 2 ; 0 ) , A D → ( 1 ; − 2 ; 0 ) , A B → = − A D → ⇒ A , B , D thẳng hàng
Cứ 3 điểm không thẳng hàng cho ta một mặt phẳng
Số cách chọn 3 trong 5 điểm trên là C 5 3 = 10
A,B,D thẳng hàng nên qua 3 điểm này không xác định được mặt phẳng
Số cách chọn 2 trong và điểm A,B,D và 1 điểm trong O và C là: C 3 2 . C 2 1 = 6
Nếu chọn 2 trong 3 điểm A,B,D kết hợp cùng hai điểm còn lại sẽ ra một số mặt phẳng trùng nhau. Nên trường hợp này ta chỉ xác định được 2 mặt phẳng phân biệt
Vậy số mặt phẳng phân biệt đi qua 3 điểm O,A,B,C,D là: 10 - 1 - 6 + 2 = 5