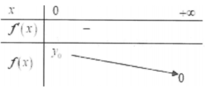
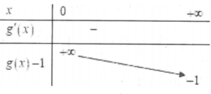
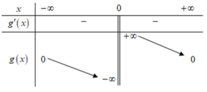
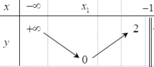
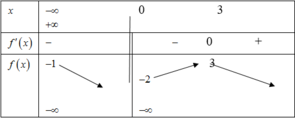
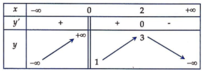
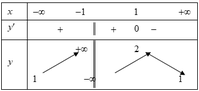
Cho các hàm số y = f x và y = g x liên tục trên mỗi khoảng xác định của chúng và có bảng biến thiên được cho như hình vẽ dưới đây
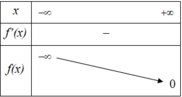
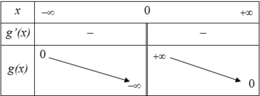
Mệnh đề nào dưới đây sai?
A. Phương trình f x = g x không có nghiệm thuộc khoảng - ∞ ; 0
B. Phương trình f x + g x = m có hai nghiệm với mọi m > 0
C. Phương trình f x + g x = m có nghiệm với mọi m
D. Phương trình f x = g x - 1 không có nghiệm

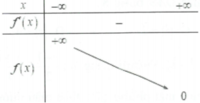
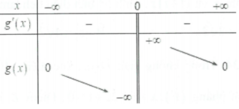
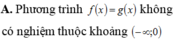
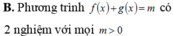

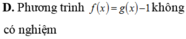









Chọn đáp án D
Trong khoảng - ∞ ; 0
ta có f x > 0 và g x < 0 nên phương trình f x = g x vô nghiệm. Phương án A đúng.
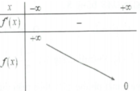
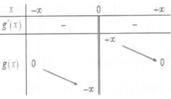
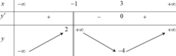
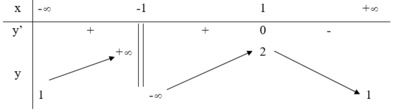
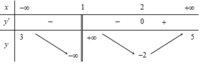
Đặt h x = f x + g x
Ta có bảng biến thiên:
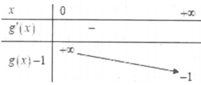
Xét hai hàm số y 1 = f x và y 2 = g x - 1 trên khoảng 0 ; + ∞
Suy ra phương trình f x = g x - 1 có ít nhất một nghiệm trên 0 ; + ∞ . Phương án D sai.