x-1=0
căn (x-1)=0
cho e hỏi 2 phương trình này có phải 1 phương trình tương đương không, vì sao ạ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hai phương trình \(x - 1 = 0\)và \(\frac{{{x^2} - 1}}{{x + 1}} = 0\) có tương đương vì:
\(\begin{array}{l}\frac{{{x^2} - 1}}{{x + 1}} = 0\\ \Leftrightarrow \frac{{\left( {x - 1} \right).\left( {x + 1} \right)}}{{x + 1}} = 0\\ \Leftrightarrow x - 1 = 0\end{array}\)

- Phương trình x = 0 có tập nghiệm S1 = {0}.
- Xét phương trình x(x - 1) = 0. Vì một tích bằng 0 khi một trong hai thừa số bằng 0 tức là:
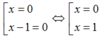
Nên phương trình này có tập nghiệm S2 = {0; 1}.
Vì S1 ≠ S2 nên hai phương trình không tương đương.

Nếu bình phương hai vế (khử căn thức chứa ẩn) của bất phương trình 1 - x ≤ x ta nhận được bất phương trình 1 - x ≤ x 2
Bất phương trình nhận được không tương đương với bất phương trình đã cho vì có x = 2 không phải là nghiệm bất phương trình đã cho nhưng lại là nghiệm của bất phương trình mới nhận được sau phép bình phương.
Ghi nhớ: Không được bình phương hai vế một bất phương trình vì có thể làm xuất hiện nghiệm ngoại lai.

Giải pt \(\dfrac{x}{3}+1=0\)
\(\Leftrightarrow\dfrac{x}{3}=-1\Leftrightarrow x=-1.3\Leftrightarrow x=-3\)
Vậy 2 pt đó tương đương nhau
`x/3 +1 = 0`
`<=> x/3 = -1`
`<=> x=-3.`
Vậy `2` phương trình tương đương với nhau


Hai phương trình này không tương đương vì chúng không có chung tập nghiệm