Cho phương trình . Giải phương trình trong mỗi trường hợp sau: m = 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khi m = -2, phương trình đac cho trở thành:
[ - 2 2 – 4]x + 2 = -2 ⇔ 0x + 2 = -2 ⇔ 0x = -4
Vậy phương trình đã cho vô nghiệm.

a)với m=2 ta có:
(22-4)x+2=2
<=>0*x+2=2
<=>0x=0
<=>x có thể nhận tất cả giá trị
b)với m=-2 ta có:
[(-2)2-4)x+2=2
tương tự như phần a
c)với m=-2,2 ta có:
[(-2,2)2-4]x+2=-2,2
<=>4,84*x+2=-2,2
<=>4,84*x=-4,2
<=>x=.. tự tính
a)với m=2 ta có:
(22-4)x+2=2
<=>0*x+2=2
<=>0x=0
<=>x có thể nhận tất cả giá trị
b)với m=-2 ta có:
[(-2)2-4)x+2=2
tương tự như phần a
c)với m=-2,2 ta có:
[(-2,2)2-4]x+2=-2,2
<=>4,84*x+2=-2,2
<=>4,84*x=-4,2
<=>x=.. tự tính
Ai k mk mk k lại

Giải:
a. Khi m = 2, phương trình đã cho trở thành:
(22−4)x+2=2⇔0x+2=2⇔2=2(22−4)x+2=2⇔0x+2=2⇔2=2
Vậy phương trình đã cho có vô số nghiệm.
b. Khi m = -2, phương trình đã cho trở thành:
[(−2)2−4]x+2=−2⇔0x+2=−2⇔0x=−4[(−2)2−4]x+2=−2⇔0x+2=−2⇔0x=−4
Vậy phương trình đã cho vô nghiệm.
c. Khi m = -2,2, phương trình đã cho trở thành:
[(−2,2)2−4]x+2=−2,2⇔0,84x+2=−2,2⇔0,84x=−2,2−2⇔0,84x=−4,2⇔x=−5[(−2,2)2−4]x+2=−2,2⇔0,84x+2=−2,2⇔0,84x=−2,2−2⇔0,84x=−4,2⇔x=−5
Vậy phương trình đã cho có nghiệm x = -5
mấy bài giải phương trình kiểu vầy ko ai giỏi hơn casio và vinacal đâu. hé hé :)))

Giải:
a. Khi m = 2, phương trình đã cho trở thành:
(22−4)x+2=2⇔0x+2=2⇔2=2(22−4)x+2=2⇔0x+2=2⇔2=2
Vậy phương trình đã cho có vô số nghiệm.
b. Khi m = -2, phương trình đã cho trở thành:
[(−2)2−4]x+2=−2⇔0x+2=−2⇔0x=−4[(−2)2−4]x+2=−2⇔0x+2=−2⇔0x=−4
Vậy phương trình đã cho vô nghiệm.
c. Khi m = -2,2, phương trình đã cho trở thành:
[(−2,2)2−4]x+2=−2,2⇔0,84x+2=−2,2⇔0,84x=−2,2−2⇔0,84x=−4,2⇔x=−5[(−2,2)2−4]x+2=−2,2⇔0,84x+2=−2,2⇔0,84x=−2,2−2⇔0,84x=−4,2⇔x=−5
Vậy phương trình đã cho có nghiệm x = -5

Khi m = -2,2, phương trình đã cho trở thành:
[ - 2 , 2 2 – 4]x + 2 = -2,2 ⇔ 0,84x + 2 = -2,2
⇔ 0,84x = -2,2 – 2 ⇔ 0,84x = -4,2 ⇔ x = -5
Vậy phương trình đã cho có nghiệm x = -5.

Bài 9:
Không, vì $x+2=0$ có nghiệm duy nhất $x=-2$ còn $\frac{x}{x+2}=0$ ngay từ đầu đkxđ đã là $x\neq -2$ (cả 2 pt không có cùng tập nghiệm)
Bài 8:
a. Khi $m=2$ thì pt trở thành:
$(2^2-9)x-3=2$
$\Leftrightarrow -5x-3=2$
$\Leftrightarrow -5x=5$
$\Leftrightarrow x=-1$
b.
Khi $m=3$ thì pt trở thành:
$(3^2-9)x-3=3$
$\Leftrightarrow 0x-3=3$
$\Leftrightarrow 0=6$ (vô lý)
c. Khi $m=3$ thì pt trở thành:
$[(-3)^2-9]x-3=-3$
$\Leftrightarrow 0x-3=-3$ (luôn đúng với mọi $x\in\mathbb{R}$)
Vậy pt vô số nghiệm thực.

Theo bài ra ta có : \(\left(m-1\right)\left(m-2\right)x=-m+2\)
\(\Leftrightarrow\left(m-1\right)\left(m-2\right)x=-\left(m-2\right)\)
\(\Leftrightarrow\left(m-1\right)\left(m-2\right)x+\left(m-2\right)=0\)
\(\Leftrightarrow\left(m-2\right)\left[\left(m-1\right)x+1\right]=0\)
a, Thay m = 1 vào phương trình trên :
\(\Leftrightarrow-1.1=0\Leftrightarrow-1\ne0\)
Vậy phương trình vô nghiệm
b, Thay m = 2 vào phương trình trên :
\(\Leftrightarrow0\left[\left(2-1\right)x+1\right]=0\Rightarrow0=0\)
c, Thay m = 0 vào phương trình trên :
\(\Leftrightarrow-2\left[\left(0-1\right)x+1\right]=0\)
\(\Leftrightarrow-2\left(-x+1\right)=0\Leftrightarrow x=1\)
Vậy tập nghiệm của phương trình là S = { 1 }

Xét (I): 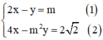
Từ phương trình (1) ta rút ra được y = 2x – m (*)
Thay (*) vào phương trình (2) ta được:
4x – m2.(2x – m) = 2√2
⇔ 4x – 2m2.x + m3 = 2√2
⇔ (4 – 2m2).x = 2√2 – m3 (**)
a) Với m = -√2, phương trình (**) trở thành: 0x = 4√2
Phương trình vô nghiệm.
Vậy với m = -√2, hệ phương trình (I) vô nghiệm.
b) Với m = √2, phương trình (**) trở thành: 0x = 0
Phương trình nghiệm đúng với mọi x ∈ R, khi đó y = 2x – √2
Vậy với m = √2, hệ (I) có vô số nghiệm dạng (x ; 2x - √2), x ∈ R
c) Với m = 1, phương trình (**) trở thành: 2x = 2√2 – 1 ⇔ 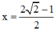
Thay vào (*) ta được:
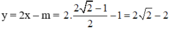
Vậy hệ phương trình có nghiệm duy nhất 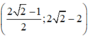
Khi m = 2, phương trình đã cho trở thành:
( 2 2 – 4)x + 2 = 2 ⇔ 0x + 2 = 2 ⇔ 2 = 2
Vậy phương trình đã cho có vô số nghiệm.