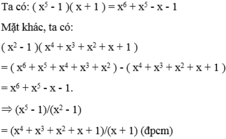Chứng minh các đẳng thức sau: ( x 3 - 1 ) ( x - 1 ) = x 2 + x + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

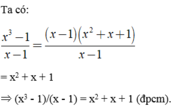

x^5- 1/ x-1= x^4+ x^3+ x^2+ x+ 1
<=> x^5 - 1 = (x - 1)(x^4 + x^3 + x^2 + x + 1)
<=> x^5 - 1 = x^5 + x^4 + x^3 + x^2 + x - x^4 - x^3 - x^2 - x - 1
<=> x^5 - 1 = x^5 - 1 (đúng)
=> đpcm
Viết lại cho vui ạ:))
\(\dfrac{x^5-1}{x-1}=x^4+x^3++x^2+x+1\\ \Leftrightarrow x^5-1=\left(x-1\right)\left(x^4+x^3+x+1\right)\\ \Leftrightarrow x^5-1=x^5+x^4+x^3+x^2+x-x^4-x^3-x^2-x-1\\ \Leftrightarrow x^5-1=x^5-1\left(đpcm\right)\)


\(VT=\dfrac{x^2+xy+2xy+2y^2}{x^2\left(x+2y\right)-y^2\left(x+2y\right)}=\dfrac{\left(x+y\right)\left(x+2y\right)}{\left(x+2y\right)\left(x-y\right)\left(x+y\right)}=\dfrac{1}{x-y}\)

a) \(A=\left(3x-2\right)\left(3x+2\right)-\left(3x+1\right)^2-3.\left(-2x-1\right)\)
\(=\left(3x\right)^2-4-\left(9x^2+6x+1\right)+6x+3\)
\(=9x^2-4-9x^2-6x-1+6x+3\)
\(=-2\) không phụ thuộc vào x
b) \(B=\left(x+1\right)\left(x-1\right)-\left(x-2\right)^2-4.\left(x+3\right)\)
\(=x^2-1-\left(x^2-4x+4\right)-\left(4x+12\right)\)
\(=x^2-1-x^2+4x-4-4x-12\)
\(=-17\)không phụ thuộc vào x.


\(a)sin^4x+cos^4x=1-2sin^2x\cdot cos^2x\)
\(\Leftrightarrow sin^4x+2sin^2x\cdot cos^2x+cos^4x=1\)
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2=1\)(luôn đúng)
a) \sin ^{4} x+\cos ^{4} x=\sin ^{4} x+\cos ^{4} x+2 \sin ^{2} x \cos ^{2} x-2 \sin ^{2} x \cos ^{2} xsin4x+cos4x=sin4x+cos4x+2sin2xcos2x−2sin2xcos2x
\begin{aligned}&=\left(\sin ^{2} x+\cos ^{2} x\right)^{2}-2 \sin ^{2} x \cos ^{2} x \\&=1-2 \sin ^{2} x \cos ^{2} x\end{aligned}=(sin2x+cos2x)2−2sin2xcos2x=1−2sin2xcos2x
b) \dfrac{1+\cot x}{1-\cot x}=\dfrac{1+\dfrac{1}{\tan x}}{1-\dfrac{1}{\tan x}}=\dfrac{\dfrac{\tan x+1}{\tan x}}{\dfrac{\tan x-1}{\tan x}}=\dfrac{\tan x+1}{\tan x-1}1−cotx1+cotx=1−tanx11+tanx1=tanxtanx−1tanxtanx+1=tanx−1tanx+1
c) \dfrac{\cos x+\sin x}{\cos ^{3} x}=\dfrac{1}{\cos ^{2} x}+\dfrac{\sin x}{\cos ^{3} x}=\tan ^{2} x+1+\tan x\left(\tan ^{2} x+1\right)cos3xcosx+sinx=cos2x1+cos3xsinx=tan2x+1+tanx(tan2x+1)
=\tan ^{3} x+\tan ^{2} x+\tan x+1=tan3x+tan2x+tanx+1

a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(=x^2+2x-5x-10+3x^2-12-3x+\dfrac{1}{2}x^2+5x^2\)
\(=\dfrac{19}{2}x^2-6x-22\)
Vậy biểu thức trên phụ thuộc vào biến x.
b) \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\)
Giải:
VT = \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3+y^2+y-y^2-y-1\)
\(=y^3-1\)
Vậy \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\).
Giải:
a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3\left(x^2-4\right)-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3x^2-12x-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=-10-18x+\dfrac{19}{2}x^2\)
Vậy biểu thức trên phụ thuộc vào biễn x
b) \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3-y^2+y^2-y+y-1\)
\(=y^3-\left(y^2-y^2\right)-\left(y-y\right)-1\)
\(=y^3-1\)
Vậy ...

\(\dfrac{x^2+1}{x}=\dfrac{x^2}{x}+\dfrac{1}{x}=x+\dfrac{1}{x}\)
Theo bất đẳng thức Cô - si, ta có:
\(x+\dfrac{1}{x}\ge2\sqrt{x.\dfrac{1}{x}}=2\sqrt{1}=2\)
Vậy \(\dfrac{x^2+1}{x}\ge2\)