Tìm số tiếp tuyến của đồ thị hàm số y = 4 x 3 - 6 x 2 + 1 , biết tiếp tuyến đó đi qua điểm M ( - 1 ; - 9 )
A. 3
B. 2
C. 0
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(y'=4x^3+2x\)
a. \(y=1\Rightarrow x^4+x^2+1=1\Rightarrow x^2\left(x^2+1\right)=0\Rightarrow x=0\Rightarrow y'=0\)
Phương trình tiếp tuyến: \(y=0\left(x-0\right)+1\Leftrightarrow y=1\)
b. \(y'\left(-1\right)=-6\)
Phương trình tiếp tuyến: \(y=-6\left(x+1\right)+3\)

\(x_0=-1\Rightarrow y_0=1-m+3m+1=2-2m\)
\(y'=4x^3-2mx\Rightarrow y'\left(1\right)=4-2m\)
\(\Rightarrow pttt:y=\left(4-2m\right)\left(x+1\right)+2-2m\)
\(A\left(0;2\right)\in pttt\Rightarrow4-2m+2-2m=2\Leftrightarrow m=1\)


Goi \(B\left(x_0;y_0\right)\) la tiep diem \(\Rightarrow x_0=1\Rightarrow y_0=3m\)
\(y'=3x^2-4x+3m\Rightarrow y'\left(1\right)=3-4+3m=3m-1\)
\(\Rightarrow pttt:y=\left(3m-1\right)\left(x-1\right)+3m\)
\(A\left(1;3\right)\in pttt\Rightarrow\left(3m-1\right)\left(1-1\right)+3m=3\Leftrightarrow3m=3\Leftrightarrow m=1\)

- Hàm số đã cho xác định với ∀x ∈ R.
- ta có:
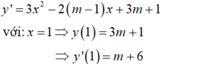
- Phương trình tiếp tuyến tại điểm có hoành độ x = 1 là:
y = (m+ 6)(x – 1) + 3m + 1
- Tiếp tuyến này đi qua A(2; - 1) nên có:
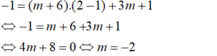
- Vậy m = -2 là giá trị cần tìm.

\(x_0=1\Rightarrow y_0=1-m\)
\(y'=\dfrac{\left(mx-1\right)'\left(x-2\right)+\left(mx-1\right)\left(x-2\right)'}{\left(x-2\right)^2}=\dfrac{mx-2m+mx-1}{\left(x-2\right)^2}\)
\(\Rightarrow y'\left(1\right)=m-2m+m-1=-1\)
\(\Rightarrow pttt:y=-1\left(x-1\right)+1-m\)
\(A\left(1;-2\right)\in pttt\Rightarrow-1\left(1-1\right)+1-m=-2\Leftrightarrow m=3\)

\(y'=\dfrac{3}{\left(x+1\right)^2}\Rightarrow\) phương trình tiếp tuyến tại \(M\left(m;\dfrac{m-2}{m+1}\right)\) có dạng:
\(y=\dfrac{3}{\left(m+1\right)^2}\left(x-m\right)+\dfrac{m-2}{m+1}\)
\(\Leftrightarrow3x-\left(m+1\right)^2y+m^2-4m-2=0\)
\(P=d\left(I;d\right)=\dfrac{\left|6m+6\right|}{\sqrt{9+\left(m+1\right)^4}}=\dfrac{6}{\sqrt{\left(m+1\right)^2+\dfrac{9}{\left(m+1\right)^2}}}\le\dfrac{6}{\sqrt{2\sqrt{\dfrac{9\left(m+1\right)^2}{\left(m+1\right)^2}}}}=\sqrt{6}\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left(m+1\right)^2=\dfrac{9}{\left(m+1\right)^2}\Leftrightarrow\left(m+1\right)^2=3\Rightarrow m=\) ... lại xấu :)