Trong không gian, tập hợp các điểm M nhìn đoạn thẳng cố định AB dưới một góc vuông là:
A. Tập hợp chỉ có một điểm
B. Một đường thẳng
C. Một đường tròn
D. Một mặt cầu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Gọi O là trung điểm của AB.
Tam giác AMB là vuông tại M có OM là đường trung tuyến ứng với cạnh huyền nên : 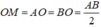
Suy ra, M thuộc mặt cầu tâm O, bán kính là 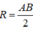
+ Ngược lại, xét mặt cầu 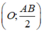 với O là trung điểm của AB.
với O là trung điểm của AB.
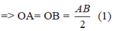
Lấy điểm M bất kì thuộc mặt cầu này. Suy ra: 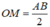 (2)
(2)
Từ (1) và (2) suy ra:
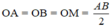
⇒ Tam giác MAB vuông tại M.
Kết luận: Vậy tập hợp các điểm M trong không gian luôn nhìn đoạn thẳng AB cố định dưới 1 góc vuông là mặt cầu 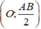

Gọi O là trung điểm đoạn thẳng AB, vì tam giác AMB vuông tại M nên trung tuyến MO bằng nửa cạnh huyến, tức MO = AB/2 = R.
Vậy tập hợp các điểm M nhìn AB dwói một góc vuông nằm trêm mặt càu đường kính AB
Ngược lại, lấy M thuốc mặt cầu đwòng kính AB thì MO = AB/2 do đó nếu M khác A và B thì tam giác MAB vuông tại M, còn khi M = A hoặc M = B ta cũng coi M nhìn AB một góc vuông.
Kết luận: Tập hợp các điểm M trong không gian nhín đoạn thẳng AB dưới một góc vuông là mặt cầu đương kính AB


![]()
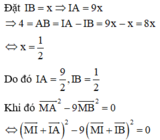
⇔ M I 2 + 2 M I → . I A → + I A 2 − 9 M I 2 + 2 M I → . I B → + I B 2 = 0 ⇔ M I 2 + I A 2 − 9 M I 2 − 9 I B 2 + 2 M I → I A → − 9 I B → = 0 ⇔ − 8 M I 2 + I A 2 − 9 I B 2 = 0 ⇒ − 8 M I 2 + 9 2 2 − 9. 1 2 2 = 0 ⇔ − 8 M I 2 = − 18 ⇔ M I 2 = 9 4 ⇔ M I = 3 2
Vậy M nằm trên mặt cầu tâm I bán kính M I = 3 2
Chọn: D

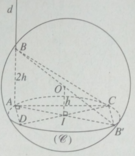
Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).
Đáp án B
Gọi O là trung điểm của đoạn thẳng AB, ta có:
M / A M ⏜ B = 90 ° = M / OM = AB 2 = S O ; AB 2
Vậy tập hợp các điểm M nhìn đoạn thẳng cố định AB dưới một góc vuông là mặt cầu tâm O bán kính R = AB 2 .