Thể tích của khối chóp tam giác đều có cạnh đáy bằng 2a và chiều cao bằng 3 a là
A. 3 a 3
B. 4 3 a 3
C. a 3
D. 4 a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

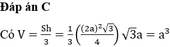

Diện tích đáy lớn là: \(S = \frac{{{{\left( {2{\rm{a}}} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Diện tích đáy bé là: \(S' = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích của bồn chứa là: \(V = \frac{1}{3}.\frac{{a\sqrt 6 }}{3}\left( {{a^2}\sqrt 3 + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} + \frac{{{a^2}\sqrt 3 }}{4}} \right) = \frac{{7\sqrt 2 }}{{12}}{a^3}\)
Chọn C.

Đáp án D
Gọi M là trung điểm của BC, H là chân đường vuông góc kẻ từ A đến SM. Khi đó khoảng cách từ A đến mặt phẳng (SBC) bằng AH. Ta có:


gọi các cạnh đáy của hình chóp là ABC vì ΔABC đều => AB=AC=BC=4cm
kẻ đường thẳng đi qua A ⊥ BC tại M
=> AM là đường cao của tam giác => \(\widehat{AMB}=\)90o
=> AM là đường trung tuyến ( tc Δ đều)
=> BM=CM=BC/2=4/2=2cm
xét ΔAMB có \(\widehat{AMB}=\)90o
=> AM2+BM2=AB2 (đl pitago)
=>AM2+22=42
=> AM=\(2\sqrt{3}\)
=> V của hình chóp = \(\dfrac{2\sqrt{3}.4}{2}.6.\dfrac{1}{3}\)=\(8\sqrt{3}\)cm3 => Đáp án B

Đáp án C

Gọi H là trực tâm của tam giác đều ABC ⇒ S H ⊥ A B C
A H = 2 3 a 3 2 = a 3 3 S H = S A 2 − A H 2 = 3 a 2 − a 2 3 = 2 6 a 3 V S . A B C = 1 3 S H . S A B C = 1 3 2 6 a 3 a 2 3 4 = a 3 2 6