Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a, chiều cao bằng 2a. Tính cosin của góc tạo bởi hai đường thẳng AC và BC’.
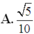
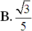
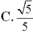
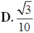
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Bán kính đường tròn đáy r = B C 2 sin A = a 3
Bán kính mặt cầu ngoại tiếp lăng trụ R = h 2 2 + r 2 = 2 a 3 ⇒ V = 4 3 π R 3 = 32 3 π a 3 27 .

Đáp án B
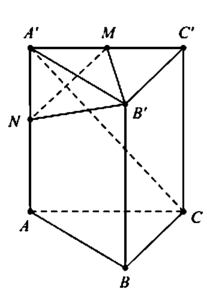 Gọi M là trung điểm A’C’. Ta có
B
'
M
⊥
A
C
C
'
A
'
⇒
B
'
M
⊥
A
'
C
.
Gọi M là trung điểm A’C’. Ta có
B
'
M
⊥
A
C
C
'
A
'
⇒
B
'
M
⊥
A
'
C
.
Suy ra M ∈ m p P . Kẻ M N ⊥ A ' C ( N ∈ A A ' ) ⇒ N ∈ m p P
Thiết diện cắt bởi mặt phẳng (P) và lăng trụ là tan giác B’MN
Hai tam giac A’C’C và NA’M đồng dạng ⇒ A ' N = 1 2 A ' M = a 4
Thể tích tứ diện A'B'MN là V 1 = 1 3 A ' N . S ∆ A ' B ' M = a 3 3 96
Thể tích lăng trụ là V = A A ' . S ∆ A B C = a 3 3 2 . Vậy V 1 V 2 = 1 47 .

Đáp án A
Khoảng cách giữa hai mặt đáy là h = AH = A’H.tan A A ' H ^ = a 3 2 . tan 30 0 = a 2
Đáp án A.