Một khối nón có bán kính đáy bằng 2cm, chiều cao bằng 3 cm. Một mặt phẳng đi qua đỉnh và tạo với đáy một góc 60 ° chia khối nón làm 2 phần. Tính thể tích V phần nhỏ hơn (Tính gần đúng đến hàng phần trăm).
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
- Xác định góc giữa mặt phẳng và mặt phẳng.
- Lập tỉ lệ thể tích thông qua tỉ lệ diện tích đáy và tỉ lệ chiều cao.
Cách giải:
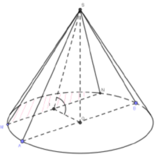
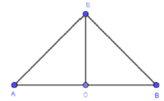
Xét hình nón (H) thỏa mãn yêu cầu đề bài, có một thiết diện qua trục là tam giác SAB.
Ta có: SAB cân tại S và là tam giác vuông cân => △ SAB vuông cân tại đỉnh S
Gọi O là trung điểm của AB 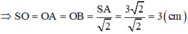
Thể tích hình nón (H): 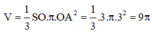
Gọi (P) là một mặt phẳng đi qua đỉnh và tạo với đáy một góc 600 thiết diện của (P) với mặt đáy là tam giác cân SMN.
Gọi I là trung điểm của MN (hiển nhiên I không trùng O), suy ra IO ⊥ MN. Mà SO ⊥ MN
![]()
Tam giác SIO vuông tại O
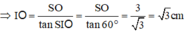
Gọi V0 là thể tích của phần nhỏ hơn. Ta có: 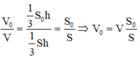
*) Tính diện tích đáy của phần có thể tích nhỏ hơn:
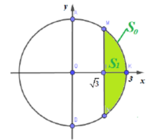
Diện tích hình tròn
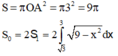
Đặt ![]()
Đổi cận:
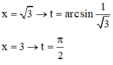
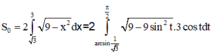
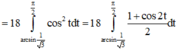
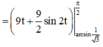

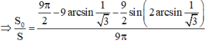
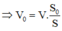
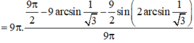
![]()