Cho biểu thức L = 1- z+ z2- z3+ ...+ z2016- z2017 với 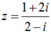. Biểu thức L có giá trị là A. 1 - i. B. 1 + i. ...
Đọc tiếp
Cho biểu thức L = 1- z+ z2- z3+ ...+ z2016- z2017 với 
. Biểu thức L có giá trị là
A. 1 - i.
B. 1 + i.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PT
1
Những câu hỏi liên quan
CM
22 tháng 5 2018
Đáp án C.
Ta có z − 1 2 z − i 4 = 1 ⇔ z − 1 4 − 2 z − i 4 = 0 . Đặt f z = z − 1 4 − 2 z − 1 4 . Phương trình f z = 0 có 4 nghiệm nên f z = 15 z − z 1 z − z 2 z − z 3 z − z 4
Do i 2 = − 1 nên z 2 + 1 = z 2 − i 2 = z − i z + i . Từ đó ta có:
P = z 1 − i z 2 − i z 3 − i z 4 − i . z 1 + i z 2 + i z 3 + i z 4 + i
= i − z 1 i − z 2 i − z 3 i − z 4 . − i − z 1 − i − z 2 − i − z 3 − i − z 4
⇒ P = f i 15 . f − i 15 = i − 1 4 − 2 i − 1 4 15 . − i − 1 4 − − 2 i − 1 4 15 = 13 5
CM
23 tháng 3 2017
Ta có
z = - 1 + 3 i 2 ⇒ 2 z + 1 = 3 i ⇒ 2 x + 1 2 = - 3
hay z 2 + z + 1 = 0 ⇔ z + 1 z = - 1
Khi đó:
z 2 = 1 z 2 = z + 1 z 2 - 2 = - 1 z 3 = 1 z 3 = z + 1 z 3 - 3 z + 1 z = 2 z 4 = 1 z 4 = z 2 + 1 z 2 - 2 = - 1
Như vậy
P = - 1 2016 + - 1 2017 + 2 2018 + - 1 2019 - 2 2018 = - 1
Đáp án D
30 tháng 1 2021
Sửa đề: \(P=x^{2008}+y^{2009}+z^{2010}\)
Ta có: x+y+z=1
nên \(\left(x+y+z\right)^3=1\)
\(\Leftrightarrow x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(x+z\right)=1\)
\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(z+x\right)+1=1\)
\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)
mà 3>0
nên \(\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y=0\\y+z=0\\x+z=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-y\\y=-z\\x=-z\end{matrix}\right.\)
Thay x=-y vào biểu thức \(x+y+z=1\), ta được:
\(-y+y+z=1\)
hay z=1
Thay x=-y và z=1 vào biểu thức \(x^2+y^2+z^2=1\), ta được:
\(\left(-y\right)^2+y^2+1=1\)
\(\Leftrightarrow y^2+y^2=0\)
\(\Leftrightarrow2y^2=0\)
hay y=0
Vì x=-y
và y=0
nên x=0
Thay x=0; y=0 và z=1 vào biểu thức \(P=x^{2008}+y^{2009}+z^{2010}\), ta được:
\(P=0^{2008}+0^{2009}+1^{2010}=1\)
Vậy: P=1
TT
12 tháng 11 2022
nma ở trên cm y=-z mà. Nếu ở thay y=0 và z=1 vào thì nghĩa là 0 = -1 hả
CM
11 tháng 1 2018
Đáp án D.
Gọi M a ; b là điểm biểu diễn số phức z = a + b i . Đặt I = 1 ; 1 , A 7 ; 9 và B 0 ; 8
Ta xét bài toán: Tìm điểm M thuộc đường tròn C có tâm I, bán kính R = 5 sao cho biểu thức P = M A + 2 M B đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm K x ; y sao cho M A = 2 M K ∀ M ∈ C .
Ta có
M A = 2 M K ⇔ M A 2 = 4 M K 2 ⇔ M I → + I A → 2 = 4 M I → + I K → 2
⇔ M I 2 + I A 2 + 2 M I → . I A → = 4 M I 2 + I K 2 + 2 M I → . I K →
⇔ 2 M I → I A → − 4 I K → = 3 R 2 + 4 I K 2 − I A 2 *
(*) luôn đúng ∀ M ∈ C ⇔ I A → − 4 I K → = 0 → 3 R 2 + 4 I K 2 − I A 2 = 0 .
I A → − 4 I K → = 0 → ⇔ 4 x − 1 = 6 4 y − 1 = 8 ⇔ x = 5 2 y = 3
Thử trực tiếp ta thấy K 5 2 ; 3 thỏa mãn 3 R 2 + 4 I K 2 − I A 2 = 0 .
Ta cos M A + 2 M B = 2 M K + 2 M B = 2 M K + M B ≥ 2 K B .
Vì B I 2 = 1 2 + 7 2 = 50 > R 2 = 25 nên B nằm ngoài (C).
Vì K I 2 = 3 2 2 + 2 2 < R 2 = 25 nên K nằm trong (C) .
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi M thuộc đoạn thẳng BK . Do đó M A + 2 M B nhỏ nhất khi và chỉ khi M là giao điểm của (C) và đường thẳng BK.
Phương trình đường thẳng B K : 2 x + y − 8 = 0 .
Phương trình đường tròn C : x − 1 2 + y − 1 2 = 25 .
Tọa độ điểm M là nghiệm của hệ
2 x + y = 8 x − 1 2 + y − 1 2 = 25 ⇔ x = 1 y = 6
hoặc x = 5 y = − 2 .
Thử lại thấy M 1 ; 6 thuộc đoạn BK.
Vậy a = 1, b = 6 ⇒ a + b = 7 .
Chọn A.
+ Ta có:
+ Khi đó: L = 1- z+ z2- z3+ ...+ z2016- z2017