Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có g ' x = 2 x 1 ln x 2 - 1 ln x = x - 1 ln > 0 , ∀ x > 1 ⇒ g(x) đồng biến trên 1 ; + ∞
Suy ra tập giá trị của hàm số g(x) là T = g 1 + ; g + ∞
Do 1 ln t là hàm số nghịch biến nên g x ≥ x 2 - x 1 ln x 2 → + ∞ khi x → + ∞
Do đó g + ∞ = + ∞
Để tính g 1 + đặt t = e x , ta được g x = ∫ ln x 2 ln x e v v d v
Khi đó g x < e 2 ln x = ∫ ln x 2 ln x d v v = x 2 ln 2
Chứng minh tương tự, ta thu được g(x) > xln(2)
Theo định lí kẹp, ta suy ra g 1 + = ln 2
Vậy tập giá trị của hàm số đã cho là T = ln 2 ; + ∞
Đáp án D
Chọn D.
Ta có: TXĐ D = [1;9]
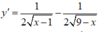
Cho y' = 0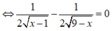 
Ta có: 
Vậy tập giá trị của hàm số là [2 2 ;4]
Đáp án D