Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = a. Gọi I là trung điểm của AC. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H thỏa mãn
B
I
→
= 3
I
H
→
. Góc giữa hai mặt phẳng (SAB) và (SBC) là 60 độ. Thể tích của khối chóp S.ABC là: A. V = a3/9 B.V = a3/6 C.V = a3/18 D.V...
Đọc tiếp
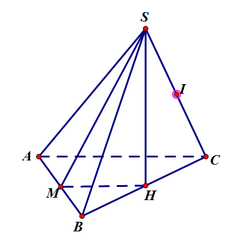
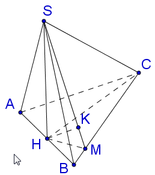
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = a. Gọi I là trung điểm của AC. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H thỏa mãn B I → = 3 I H → . Góc giữa hai mặt phẳng (SAB) và (SBC) là 60 độ. Thể tích của khối chóp S.ABC là:
A. V = a3/9
B.V = a3/6
C.V = a3/18
D.V = a3/3
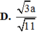
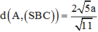
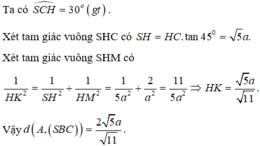
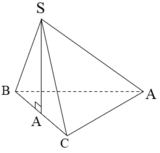
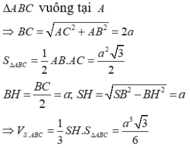
Chọn A
Cách 1:
Dễ thấy hai tam giác SAB và SAC bằng nhau (cạnh chung SA), gọi K là chân đường cao hạ từ A trong tam giác SAB
Từ giả thiết tam giác ABC vuông cân tại B ta được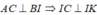
Trong tam giác ICK vuông tại I có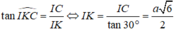
.
Như vậy Ik > IB (vô lý).
TH2: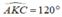
tương tự phần trên ta có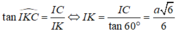 
Do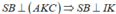
nên tam giác BIK vuông tại K và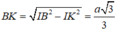 
Như vậy tam giác BKI đồng dạng với tam giác BHS suy ra: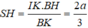
Vậy thể tích của khối chóp S.ABC là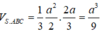
Cách 2: dùng phương pháp tọa độ hóa.