Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A B C D H K S
Hạ \(SH\perp BC\Rightarrow\left(SBC\right)\perp\left(ABC\right)\)
\(\Rightarrow SH\perp BC;SH=SB.\sin\widehat{SBC}=a\sqrt{3}\)
Diện tích : \(S_{ABC}=\frac{12}{\boxtimes}BA.BC=6a^2\)
Thể tích : \(V_{s.ABC}=\frac{1}{3}S_{ABC}.SH=2a^3\sqrt{3}\)
Hạ \(HD\perp AC\left(D\in AC\right),HK\perp SD\left(K\in SD\right)\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H,\left(SAC\right)\right)\)
\(BH=SB.\cos\widehat{SBC}=3a\Rightarrow BC=4HC\)
\(\Rightarrow d\left(B,\left(SAC\right)\right)=4d\left(H,SAC\right)\)
Ta có : \(AC=\sqrt{BA^2+BC^2}=5a;HC=BC-BH=a\)
\(\Rightarrow HD=BA.\frac{HC}{AC}=\frac{3a}{5}\)
\(HK=\frac{SH.HS}{\sqrt{SH^2+HD^2}}=\frac{3a\sqrt{7}}{14}\)
Vậy \(d\left(B,\left(SAC\right)\right)=4HK=\frac{6a\sqrt{7}}{7}\)
1.
\(V=\frac{1}{3}SA.\frac{1}{2}AB.BC=\frac{1}{6}.a.a.2a=\frac{a^3}{3}\)
2.
\(V=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}.2a\sqrt{3}.\frac{a^2\sqrt{3}}{4}=\frac{a^3}{2}\)
P/s: chóp này là chóp "có đáy là tam giác đều" chứ không phải "chóp tam giác đều"
Hai loại này khác xa nhau đấy, ko lộn xộn nhầm lẫn được đâu
3.
Câu này đề sai
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\Rightarrow\Delta SAC\) vuông tại A
\(\Rightarrow SC>SA\) (cạnh huyền luôn lớn hơn cạnh góc vuông)
Do đó đề cho \(SA=SC\) là vô lý
4.
\(AC=BD=\sqrt{AB^2+AD^2}=2a\)
\(\widehat{SCA}=60^0\Rightarrow SA=SC.tan60^0=2a\sqrt{3}\)
\(V=\frac{1}{3}SA.AB.AD=\frac{1}{3}.2a\sqrt{3}.a.a\sqrt{3}=2a^3\)
Kẻ SH vuông góc với BC tại H => SH vuông góc với (ABC)
Kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N
Ta có góc SMH = góc SNH = 60 độ
Dễ thấy tam giác SHM = tam giác SHN => HM = HN
Ta có HM = HB.sin 30 = 1/2 HB hay HB = 2 HM
HN = HC.sin 60 = HC.căn 3 /2 => HC = 2/căn 3.HN = 2/căn 3 .HM
=> BC = a = HB + HC = ( 2 + 2/căn 3).HM
=> HM = a/(2 + 2/căn 3) = a.căn 3 /(2+ 2.căn 3)
=> SH = HM.tan 60 = 3a/(2+2.căn 3)
Có AB = BC/2 = a/2
AC = BC.căn 3/2 = a.căn 3/2
S(ABC) = 1/2.AB.AC = 1/8.a^2.căn 3
=> V(SABC) = 1/3.3a/(2+2.căn 3) . 1/8.a^2.căn 3 = a^3.căn 3 /[16.(1+ căn 3)]
4.
Qua G kẻ đường thẳng song song AB lần lượt cắt AC và BC tại M và N
\(\Rightarrow A'B'NM\) là thiết diện của (A'B'G) và lăng trụ
Theo Talet ta có \(\frac{CM}{AC}=\frac{CN}{BC}=\frac{2}{3}\Rightarrow CM=CN=\frac{2a}{3}\)
Kéo dài A'M, B'N, C'C đồng quy tại P (theo tính chất giao tuyến 3 mặt phẳng)
Do \(CN//B'C'\Rightarrow\frac{PC}{PC'}=\frac{CN}{B'C'}=\frac{2}{3}\Rightarrow\frac{PC}{PC+CC'}=\frac{2}{3}\)
\(\Rightarrow3PC=2\left(PC+a\right)\Rightarrow PC=2a\)
\(\Rightarrow PC'=3a\)
\(MN=\frac{2}{3}BC\Rightarrow S_{CMN}=\frac{4}{9}S_{ABC}=\frac{4}{9}.\frac{a^2\sqrt{3}}{4}=\frac{a^2\sqrt{3}}{9}\)
\(V_{P.A'B'C'}=\frac{1}{3}PC'.S_{A'B'C'}=\frac{1}{3}.3a.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{4}\)
\(V_{P.CMN}=\frac{1}{3}PC.S_{CMN}=\frac{1}{3}.2a.\frac{a^2\sqrt{3}}{9}=\frac{2a^3\sqrt{3}}{27}\)
\(\Rightarrow V_{CMN.A'B'C'}=\frac{a^3\sqrt{3}}{4}-\frac{2a^3\sqrt{3}}{27}=\frac{19a^3\sqrt{3}}{108}\)
\(\Rightarrow V_{MNABA'B'}=\frac{a^3\sqrt{3}}{4}-\frac{19a^3\sqrt{3}}{108}=\frac{2a^3\sqrt{3}}{27}\)
2.
Đề thiếu dữ kiện ko tính được, chỉ tính được trong trường hợp tam giác ABC là vuông cân.
3.
\(AC=BC=a\sqrt{2}\) ; \(AC=AB\sqrt{2}=2a\)
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\Rightarrow BM\perp\left(ACC'A'\right)\)
\(\Rightarrow\widehat{BA'M}\) là góc giữa A'B và (ACC'A')
\(\Rightarrow\widehat{BA'M}=30^0\)
\(BM=\frac{1}{2}AC=a\)
\(tan\widehat{BA'M}=\frac{BM}{A'M}\Rightarrow A'M=\frac{BM}{tan30^0}=a\sqrt{3}\)
\(A'A=\sqrt{A'M^2-AM^2}=a\sqrt{2}\)
\(V=\frac{1}{2}A'A.AB.BC=a^3\sqrt{2}\)
Ko đáp án nào đúng
4.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AH\)
Mà \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\)
Lại có \(AK\perp SC\)
\(\Rightarrow SC\perp\left(AKH\right)\Rightarrow SK\) là đường cao của chóp S.AHK ứng với đáy là tam giác AHK vuông tại H (do \(AH\perp\left(SBC\right)\Rightarrow AH\perp HK\))
Áp dụng hệ thức lượng:
\(\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AB^2}=\)
À thôi đến đây phát hiện ra đề bài sai
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AB\Rightarrow\) tam giác SAB vuông tại A với SA là cạnh góc vuông, SB là cạnh huyền
\(\Rightarrow SB>SA\Rightarrow SB=SA=a\) là hoàn toàn vô lý
A B E F C S
Gọi E là trung điểm của AC \(\Rightarrow BE\perp\left(SAC\right)\rightarrow BE\perp SC\)
Vẽ EF vuông góc với SC tại F. Ta có \(SC\perp BF\Rightarrow\widehat{EFB}=60^0\) là góc giữa (SAC) và (SBC)
Tam giác BEF vuông tại E nên \(EF=\frac{a\sqrt{2}}{2\sqrt{3}}\)
Tam gics SAC đồng dạng với tam giác EFC suy ra \(\sqrt{3}SA=SC\Leftrightarrow SA=a\)
Thể tích \(V=\frac{1}{3}S_{ABC}.SA=\frac{a^2}{6}\)
Gọi O là giao điểm của AC và BD \(\Rightarrow A_1O\perp\left(ABCD\right)\)
Gọi E là trung điểm của AD \(\Rightarrow\begin{cases}OE\perp AD\\A_1E\perp AD\end{cases}\)
Suy ra \(\widehat{A_1EO}\) là góc giữa 2 mặt phẳng \(\left(ADD_1A_1\right)\) và \(\left(ABCD\right)\) \(\Rightarrow\widehat{A_1EO}=60^o\)
Suy ra : \(A_1O=OE.\tan\widehat{A_1EO}=\frac{AB}{2}\tan\widehat{A_1EO}=\frac{a\sqrt{3}}{2}\)
Diện tích đáy \(S_{ABCD}=AB.AD=a^2\sqrt{3}\)
Thể tích \(V_{ABCD.A'B'C'D'}=S_{ABCD}.A_1O=\frac{3a^2}{2}\)
Ta có : \(B_1C||A_1D\)\(\Rightarrow B_1C||\left(A_1CD\right)\)
\(\Rightarrow d\left(B_1,\right)\left(A_1BD\right)=d\left(C,\left(A_1BD\right)\right)=CH\)
\(\Rightarrow d\left(B_1,\right)\left(A_1BD\right)=CH=\frac{CD.CB}{\sqrt{CD^2+CB^2}}=\frac{a\sqrt{3}}{2}\)
Chọn A
Cách 1:
Dễ thấy hai tam giác SAB và SAC bằng nhau (cạnh chung SA), gọi K là chân đường cao hạ từ A trong tam giác SAB
Từ giả thiết tam giác ABC vuông cân tại B ta được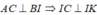
Trong tam giác ICK vuông tại I có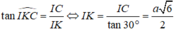
.
Như vậy Ik > IB (vô lý).
TH2: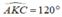
tương tự phần trên ta có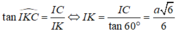 
Do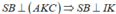
nên tam giác BIK vuông tại K và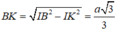 
Như vậy tam giác BKI đồng dạng với tam giác BHS suy ra: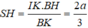
Vậy thể tích của khối chóp S.ABC là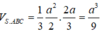
Cách 2: dùng phương pháp tọa độ hóa.