Cho hình chóp tứ giác đều S. ABCD, M là trung điểm của SC. Mặt phẳng (P) qua AM và song song với BD cắt SB, SD tại N, K. Tính tỉ số thể tích của khối S. ANMK và khối chóp S.ABCD. A. 2 9...

PT

Pham Trong Bach

18 tháng 8 2018

Cho hình chóp tứ giác đều S. ABCD, M là trung điểm của SC. Mặt phẳng (P) qua AM và song song với BD cắt SB, SD tại N, K. Tính tỉ số thể tích của khối S. ANMK và khối chóp S.ABCD. A. 2 9 B. 1 3 C. 1 2 D. 3 5 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

18 tháng 8 2018

Chọn B

Đúng(0)

PT

Pham Trong Bach

9 tháng 12 2018

Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, cạnh bên tạo với góc 60 ° . Gọi M là trung điểm của SC. Mặt phẳng qua AM và song song với BD, cắt SB, SD lần lượt tại E và F và chia khối chóp thành hai phần. Tính thể tích V của khối chóp không chứa đỉnh S. A. V = a 3 6 36 B. V = a 3 6 9 C. V = ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

9 tháng 12 2018

Chọn B.

Đúng(0)

PT

Pham Trong Bach

18 tháng 6 2018

Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 o . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD cắt SB tại E và cắt SD tại F. Tính thể tích V khối chóp S.AEMF. A. V = a 3 6 36 . B. V = a 3 6 9 . C. V = a 3 6 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

18 tháng 6 2018

Đáp án D.

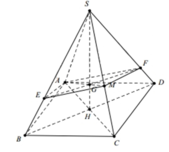
Gọi H là tâm của hình vuông A B C D ; S B H ^ = 60 0 ; H B = a 2 2

Khi đó là trọng tâm tam giác SAC.

Qua G dựng đường thẳng song song với BD cắt SB;SD lần lượt là E và F.

Do tính chất đối xứng ta có:

V S . A E M F V S . A B C D = V S . A E M V S . A B C = S E S B . S M S C = 2 3 . 1 2 = 1 3 .

Mặt khác V A . A B C D = 1 3 S H . S A B C D = 1 3 H B tan 60 0 . a 2 = a 3 6 6 .

Do đó V S . A E M F = 1 3 . a 3 6 6 = a 3 6 18 .

Đúng(0)

PT

Pham Trong Bach

7 tháng 5 2019

Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 0 . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD cắt SB tại E và cắt SD tại F. Tính thể tích V khối chóp S.AEMF ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

7 tháng 5 2019

Đúng(0)

PT

Pham Trong Bach

23 tháng 10 2019

Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 o . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD, cắt SB tại P và cắt SD tại Q. Thể tích khối chóp S.AMNQ là V. Tỉ số 18 V a 3 là ? A. 2 B. 6 C. 3 D....

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

23 tháng 10 2019

Đáp án B

Hướng dẫn giải:

Gọi H là tâm của đáy khi đó S H ⊥ ( A B C D )

Lại có S H = H A tan 60 o = a 6 2

V S . A B C D = 1 3 S H . S A B C D = a 3 6 6

Mặt khác, gọi G = S H ∩ A M

⇒ G là trọng tâm của tam giác SAC.

Do đó S G S H = 2 3

Qua G dựng đường thẳng song song với BD cắt SB, SD lần lượt tại P và Q

Khi đó V S . A B M V S . A B C = S P S B . S M S C = 1 3

từ đó suy ra V S . A P M Q V S . A B C D = 1 3

Do vậy V S . A P M Q = a 3 6 18

⇒ 18 V a 3 = 6

Đúng(0)

SG

Sách Giáo Khoa

1 tháng 4 2017

Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, cạnh bên tạo với đáy một góc \(60^0\). Gọi M là trung điểm SC. Mặt phẳng đi qua AM và song song với BD, cắt SB tại E và cắt SD tại F. Tính thể tích khối chóp S.AEMF ?

#Toán lớp 12

1

S

_silverlining

1 tháng 4 2017

ình chóp S.ABCD là hình chóp đều nên chân H của đường cao SH chính là tâm của đáy. Mặt phẳng đi qua AM và song song với BD cắt mặt phẳng (SDB) theo một giao song song với BD, hay EF // BD.

Ta dựng giao tuyến EF như sau : Gọi I là giao điểm của AM và SH Qua I ta dựng một đường thẳng song song với BD, đường này cắt SB ở E và cắt SD ở F. Ta có góc SAH= 60°. Tam giác cân SAC có SA = SC và SAC = 60° nên nó là tam giác đều: I là giao điểm của các trung tuyến AM và SH nên:

dap-an-bai-9

Đúng(0)

PT

Pham Trong Bach

13 tháng 11 2019

Cho hình chóp tứ giác đều S.ABCD . Đáy hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 o . Gọi M là trung điểm SC.Mặt phẳng đi qua AM và song song với BD, cắt SB tại E và cắt SD tại F. Tính thể tích khối chóp S.AEMF.

#Toán lớp 12

1

CM

Cao Minh Tâm

13 tháng 11 2019

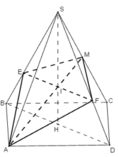
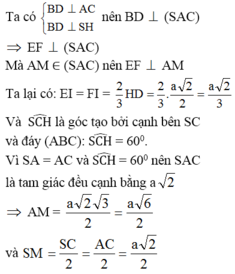
Giải bài 9 trang 26 sgk Hình học 12 | Để học tốt Toán 12

Điều này chứng tỏ SM là đường cao của hình chóp S.AEMF. Vậy thể tích của khối chóp S.AEMF là:

Đúng(0)

PT

Pham Trong Bach

6 tháng 10 2017

Cho hình chóp S.ABCD. Trên cạnh SA lấy điểm M sao cho SM = 1 3 SA . Mặt phẳng α qua M và song song với mặt đáy lần lượt cắt SB, SC, SD tại N, P, Q. Tỉ số thể tích của khối chóp S.MNPQ với khối chóp S.ABCD là A. 1 9 B. 1 3 C. 1 81 D. 1 27 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

6 tháng 10 2017

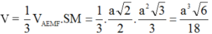
Đáp án D

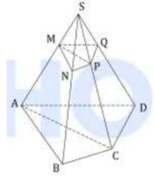
Do α qua M song song với mặt đáy nên em kẻ MN / / AB N ∈ SB ;

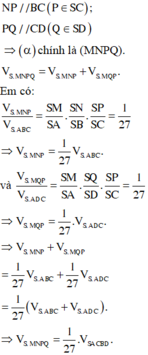
Chú ý: Em nhớ rằng, công thức tính tỉ số thể tích chỉ áp dụng cho khối chóp tam giác. Còn với khối chóp tứ giác, ngũ giác, lục giác,… em cần chia ra thành các khối chóp tam giác và áp dụng công thức.

Công thức giải nhanh:

Cắt khối chóp bởi mặt phẳng song song với đáy: Xét khối chóp S . A 1 A 2 . .. A n , mặt phẳng (P) song song với mặt đáy cắt cạnh SA 1 tại m thỏa mãn SM SA 1 = k . Khi đó (P) chia khối chóp thành 2 khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V' và khối đa diện ban đầu có thể tích V thì V ' V = k 3

Nên ⇒ V SMNPQ V SABCD = ( 1 3 ) 2 = 1 27

Đúng(0)

PT

Pham Trong Bach

8 tháng 11 2017

Cho hình chóp S.ABCD. Trên cạnh SA lấy điểm M sao cho SM= 1 3 SA. Mặt phẳng ( α ) qua M và song song với mặt đáy lần lượt cắt SB, SC, SD tại N, P, Q. Tỉ số thể tích của khối chóp S.MNPQ với khối chóp S.ABCD là A. 1 9 B. 1 3 C. 1 81 D. 1 27 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

8 tháng 11 2017

Đáp án D

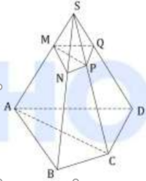
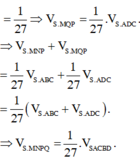
Chú ý: Em nhớ rằng, công thức tính tỉ số thể tích chỉ áp dụng cho khối chóp tam giác. Còn với khối chóp tứ giác, ngũ giác, lục giác,… em cần chia ra thành các khối chóp tam giác và áp dụng công thức.

Công thức giải nhanh:

Cắt khối chóp bởi mặt phẳng song song với đáy: Xét khối chóp S . A 1 A 2 . . . . . A n , mặt phẳng (P) song song với mặt đáy cắt cạnh S A 1 tại m thỏa mãn . Khi đó (P) chia khối chóp thành 2 khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V' và khối đa diện ban đầu có thể tích V thì V ' V = k 3

Nên ⇒ V S . M N P Q V S . A B C D = 1 3 2 = 1 27

Đúng(0)

PT

Pham Trong Bach

27 tháng 12 2019

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M di động trên cạnh SC, đặt M C M S = k . Mặt phẳng qua A, M song song với BD cắt SB, SD thứ tự tại N, P. Thể tích khối chóp C.APMN lớn nhất khi

A. k = 3 .

B. k=1

C. k=2

D. k = 2 .

#Mẫu giáo

1

CM

Cao Minh Tâm

27 tháng 12 2019

Đáp án D

Phương pháp giải:

Dùng định lí Thalet, định lý Menelaus và phương pháp tỉ số thể tích để tính thể tích khối chóp theo tham số k.

Khảo sát hàm số chứa biến k để tìm giá trị lớn nhất – giá trị nhỏ nhất

Lời giải:

Gọi O là tâm của hình bình hành ABCD và I = S O ∩ A M .

Ba điểm M,A,I thẳng hàng nên áp dụng định lý Menelaus cho tam giác SOC ta có: S M M C . C A A O . O I I S = 1 ⇒ O I S I = 1 = k 2 .

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP