Cho tam giác ABC vuông tại A , có AH là đường cao , AC = 15 cm, AB = 20 cm .
a) Tính độ dài BC , AH , số đo góc ACB
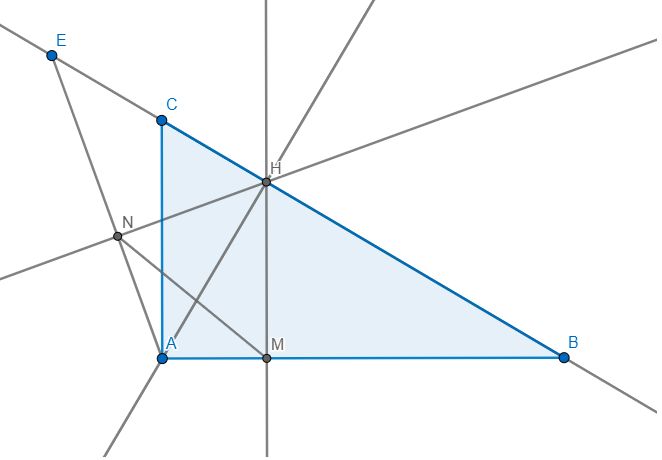
b) Từ C vẽ tia Cx vuông góc CB , tia Cx cắt tia BA tại E .
Chứng minh : AE.AB = CH.BC = BC2 - AB2
c) Gọi K là trung điểm AH , tia BK cắt CE tại M.
Chứng minh : ME = MC

a)Vì AH là đường cao cua tam giác ABC vuong tai A nen ta co :
BC^2=AB^2+AC^2=20^2+15^2=625=>BC=25(cm)
AH.BC=AB.AC=>AH=(20*15):25=12(cm)
AB=BC.cosB=>cosB=AB:BC=20:25=0,8=>góc B xấp xỉ 37 độ
b) vi CA la duong cao cua tam giác EBC vuong tai C nen ta co :
AC^2=AF.AB (1)
vi AH la duong cao cua tam giác ABC vuong tai A nen ta co:
AC^2=BC^2-AB^2 (2)
AC^2=CH.BC (3)
Tu (1),(2),(3) : suy ra
AF.AB=CH.BC=BC^2-AB^2
Có gì ko hieu ban cứ nhan tin cho minh minh se lam giúp