Tìm độ dài nhỏ nhất của cạnh một hình vuông sao cho có thể đặt vào trong nó 5 hình tròn bán kính r = 1 cm mà không có hình tròn nào có điểm trong chung.
Giúp tôi với , thanks!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
13 tháng 7 2020
Giả sử hình vuông ABCD có tâm O và cạnh a, chứa năm hình tròn không cắt nhau và đều có bán kính bằng 1
Vì cả năm hình tròn này đều nằm trọn trong hình vuông nên các tâm của chúng nằm trong hình vuông \(A'B'C'D'\)có tâm O và cạnh \(a-2\), ở đây \(A'B'//AB\)
Các đường thẳng nối các trung điểm cùa các cạnh đối diện của hình vuông \(A'B'C'D'\)chia \(A'B'C'D'\)thành 4 hình vuông nhỏ
Theo nguyên lí Dirichlet tồn tại một trong 4 hình vuông nhỏ mà trong hình vuông này chứa ít nhất hai trong số 5 tâm hình tròn nói trên (không mất tính tổng quát ta giả sử là \(O'\)và \(O''\))
Để ý rằng vì không có hai hình tròn nào (trong số năm hình tròn) cắt nhau nên \(O'O''\ge2\)
Mặt khác do \(O'\)và\(O''\)cùng nằm trong một hình vuông nhỏ (cạnh của hình vuông nhỏ đó bằng \(\frac{a-2}{2}\)) nên ta lại có \(O'O''\le\frac{a-2}{2}.\sqrt{2}\). Từ đó ta suy ra được\(\frac{a-2}{2}.\sqrt{2}\ge2\Rightarrow a\ge2\sqrt{2}+2\)
Vậy mọi hình vuông cạnh a thỏa mãn yêu cầu đề bài, ta đều có \(a\ge2\sqrt{2}+2\)
Bây giờ xét hình vuông \(ABCD\)có \(a=2\sqrt{2}+2\)
Xét năm hình tròn có tâm là \(O,A',B',C',D'\)thì mọi yêu cầu của đề bài thỏa mãn.
Tóm lại, hình vuông có kích thước bé nhất cần tìm là hình vuông với cạnh \(a=2\sqrt{2}+2\)
CM
9 tháng 11 2019
Đáp án B
Phương pháp:
- Gắn hệ trục tọa độ Oxy, xác định phương trình hàm số bậc ba.
- Ứng dụng tích phân vào tính thể tích.
Cách giải:
Gắn hệ trục tọa độ Oxy như hình vẽ.
Gọi phương trình của đường sinh là: 
Theo đề bài, ta có: (C) có điểm cực đại (0;3), điểm cực tiểu là (2;1)
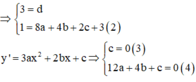
Từ (1),(2),(3) và (4)
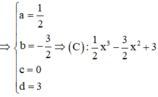
Thể tích đã cho vào:
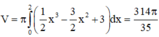
Thể tích 1 viên bi là
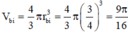
Cần số viên bi: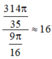 
(viên)
CM
16 tháng 7 2018
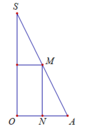
Khối trụ thu được có bán kính đáy bằng ON và chiều cao bằng MN.
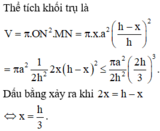
Chọn A
CM
22 tháng 11 2017
Đáp án B
Đặt SO' = x. Theo định lí Talet ta có:
x
h
=
r
'
r
0
<
x
<
h
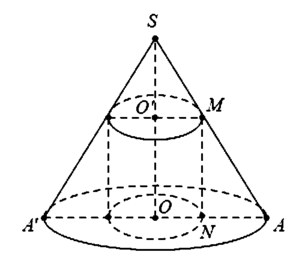
Thể tích khối trụ là V = πr ' 2 h - x = π xr 2 h 2 h - x = f x
Ta có f x = πr 2 h 2 x 2 h - x
Cách 1. Xét M x = x 2 h - x
Cách 2. Ta có M x = 4 . x 2 . x 2 . h - x ≤ 4 x 2 + x 2 + h - x 3 3 = 4 h 3 27
Dấu “=” xảy ra ⇔ x 2 = h - x ⇔ x = 2 3 h ⇒ M N = h - x = h 3 .
CM
17 tháng 8 2018
a) Hình tròn có bán kính 2cm có diện tích : S = π. 2 2 = 4π ( c m 2 )
b) Hình vuông có độ dài cạnh 3,5cm có diện tích : S = 3 , 5 2 = 12,25 ( c m 2 )
c) tam giác có các cạnh 3cm,4cm,5cm nên nó là tam giác vuông
Khi đó tam giác có diện tích: S =(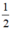
).3.4 =6(
c
m
2
)
d) Nửa mặt cầu bán kính 4cm có diện tích : S= (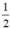
).4.
π
.
4
2
= 32
π
(
c
m
2
)
Vậy trong các hình trên thì nửa mặt cầu bán kính 4cm có diện tích lớn nhất
Vậy chọn đáp án (D)