CMR :Nếu a / b =c / d thi
5a +3b / 5a - 3b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 12 2023
\(\dfrac{a}{b}\) = \(\dfrac{c}{d}\)
\(\dfrac{a}{c}\) = \(\dfrac{b}{d}\)
\(\dfrac{a}{c}\) = \(\dfrac{5a}{5c}\) = \(\dfrac{3b}{3d}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{c}\) = \(\dfrac{5a+3b}{5c+3d}\) (1)
\(\dfrac{a}{c}\) = \(\dfrac{5a-3b}{5c-3d}\) (2)
Kết hợp (1) và (2) ta có:
\(\dfrac{5a+3b}{5c+3d}\) = \(\dfrac{5a-3b}{5c-3d}\)
⇒ \(\dfrac{5a+3b}{5a-3b}\) = \(\dfrac{5c+3d}{5c-3d}\) (đpcm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 12 2023
b; \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\)
\(\dfrac{a}{b}\) = \(\dfrac{3a}{3b}\) = \(\dfrac{2c}{2d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}\) = \(\dfrac{3a+2c}{3b+2d}\) (đpcm)
DV
0
BC
2
26 tháng 9 2015
\(\frac{a}{b}=\frac{c}{d}=>\frac{a}{c}=\frac{b}{d}=>\frac{5a}{5c}=\frac{3b}{3d}=>\frac{5a+3b}{5c+3d}=\frac{5a-3b}{5c-3d}\)
\(=>\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\left(DPCM\right)\)
26 tháng 9 2015
Từ \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{3b}{3d}=\frac{5a}{5c}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\frac{3b}{3d}=\frac{5a}{5c}=\frac{5a+3b}{5c+3d}=\frac{5a-3b}{5c-3d}\)
=> \(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\) (điều phải chứng minh)
3 tháng 1 2018
Đặt :
\(\dfrac{a}{b}=\dfrac{c}{d}=k\) \(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có :
\(\dfrac{5a+3b}{5a-3b}=\dfrac{5bk+3b}{5bk-3b}=\dfrac{b\left(5k+3\right)}{b\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\left(1\right)\)
\(\dfrac{5c+3d}{5c-3d}=\dfrac{5dk+3d}{5dk-3d}=\dfrac{d\left(5k+3\right)}{d\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrowđpcm\)
OM
3
LA
28 tháng 3 2019
Ta có
\(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\Rightarrow\left(5a+3b\right)\left(5c-3d\right)=\left(5c+3d\right)\left(5a-3b\right)\)
\(\Rightarrow25ac-15ad+15bc-9bd-25ac+15bc-15ad+9bd=0\)
\(\Rightarrow-30ad+30bc=0\)
\(\Rightarrow-30ad=-30bc\Rightarrow ad=bc\)
hay \(\frac{a}{b}=\frac{c}{d}\) ( ĐPCM)
\(\)
28 tháng 3 2019
Ta có
5a+3b5a−3b=5c+3d5c−3d⇒(5a+3b)(5c−3d)=(5c+3d)(5a−3b)5a+3b5a−3b=5c+3d5c−3d⇒(5a+3b)(5c−3d)=(5c+3d)(5a−3b)
⇒25ac−15ad+15bc−9bd−25ac+15bc−15ad+9bd=0⇒25ac−15ad+15bc−9bd−25ac+15bc−15ad+9bd=0
⇒−30ad+30bc=0⇒−30ad+30bc=0
⇒−30ad=−30bc⇒ad=bc⇒−30ad=−30bc⇒ad=bc
hay ab=cdab=cd ( ĐPCM)
LA
8 tháng 7 2017
từ a/b = c/d => a/c = b/d => 5a/5c = 3b/3d
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{5a}{5c}=\frac{3b}{3d}=\frac{5a+3b}{5c+3d}=\frac{5a-3b}{5c-3d}\)
từ: \(\frac{5a+3b}{5c+3d}=\frac{5a-3b}{5c-3d}\)áp dụng tính chất ta dc
\(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)(đcpm)
KB
2
24 tháng 8 2017
Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. lấy điểm B bất kì thuộc đường thằng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào ?
Bài giải:
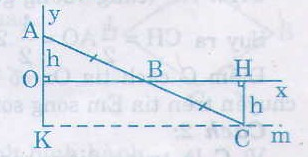
Kẻ AH và CK vuông góc với d.
Ta có AB = CB (gt)
=
( đối đỉnh)
nên ∆AHB = ∆CKB (cạnh huyền - góc nhọn)
Suy ra CK = AH = 2cm
Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.
HD
1
VM
25 tháng 10 2019
Ta có: \(\frac{a}{b}=\frac{c}{d}.\)
\(\Rightarrow\frac{a}{c}=\frac{b}{d}\)
\(\Rightarrow\frac{5a}{5c}=\frac{3b}{3d}.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{5a}{5c}=\frac{3b}{3d}=\frac{5a+3b}{5c+3d}\) (1)
\(\frac{5a}{5c}=\frac{3b}{3d}=\frac{5a-3b}{5c-3d}\) (2)
Từ (1) và (2) \(\Rightarrow\frac{5a+3b}{5c+3d}=\frac{5a-3b}{5c-3d}\left(đpcm\right).\)
Chúc bạn học tốt!
Ta có : \(\frac{a}{b}=\frac{c}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{5a}{5c}=\frac{3b}{3d}=\frac{5a+3b}{5c+3d}=\frac{5a-3b}{5c-3d}\)
=> \(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)
Đề thiếu trầm trọng