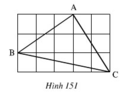
Tam giác ABC trên giấy kẻ ô vuông là tam giác gì.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
13 tháng 1 2019
Đặt độ dài cạnh ô vuông là 1 (đơn vị chiều dài)
Áp dụng định lí pitago ta có:
AB2=12+22=1+4=5
BC2=12+22=1+4=5
AC2=32+12=9+1=10
Suy ra: AC2=AB2+BC2
Áp dụng định lí pitago đảo ta có tam giác ABC vuông tại B
Lại có: AB2=BC2=5 suy ra: AB = BC. Do đó, tam giác ABC là tam giác cân tại B.
Vậy tam giác ABC vuông cân tại B
PT
1
CM
4 tháng 11 2017
Nối A với D tạo thành đường chéo ô vuông
Gọi K giao điểm AC với đỉnh ô vuông, H là giao điểm DK với đường kẻ ngang ô vuông đi qua A. ( như hình vẽ)
Ta có: ΔAHK vuông cân tại H =>∠HAK =45o
ΔAHD vuông cân tại H=>∠HAD =45o
=>∠DAK =∠HAK +∠HAD =45o+45o=90o
hay ∠DAC =90o
=>∠BAC <90o
Hình vuông có 4 góc, mỗi góc bằng 900. Từ hình vẽ suy ra: ∠ACB <90o và ∠ABC <90o
Vậy tam giác ABC là tam giác nhọn
SG
7
DN
20 tháng 4 2017
Xét tam giác ABC trên hình vẽ ta có:
AB = AC = 6 ô vuông (với điều kiện tất cả ô vuông đều bằng nhau).
=> Tam giác ABC là tam giác cân và cân tại A.
LS
0
23 tháng 1 2021
Gọi mỗi góccòn lại trên giấy ô vuông là K; M; N
Xét Tg AMB vuông tại M ta có:
AB^2 = AM^2 + MB^2 (định lí Pi-ta-go)
Thay số: AB^2 = 22 + 12 = 5
=> AB = căn 5
Xét Tg ANC vuông tại N ta có:
AC^2 = AN^2 + NC^2 (định lí Pi-ta-go )
AC^2= 32 + 42 = 25
=> AC = 5
Xét Tg BKC vuông tại K ta có:
BC^2= BK^2+ KC^2(định lí Pi-ta-go )
BC^2 = 32 + 52 = 34
=>BC= căn 34
CM
19 tháng 2 2018
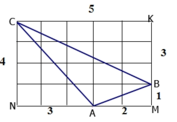
Áp dụng định lí Pi-ta-go trong ΔAMB vuông tại M ta có:
AB2 = AM2 + MB2 = 22 + 12 = 5
⇒ AB = √5
Áp dụng định lí Pi-ta-go trong ΔANC vuông tại N ta có:
AC2 = AN2 + NC2 = 32 + 42 = 25
⇒ AC = 5
Áp dụng định lí Pi-ta-go trong ΔBKC vuông tại K ta có:
BC2 = BK2 + KC2 = 32 + 52 = 34
⇒ BC = √34
Vẽ lại hình:
Áp dụng định lý Pytago :
- Trong tam giác ABH có : AB2 = AH2 + HB2 = 22 + 32 = 13.
- Trong tam giác AKC có : AC2 = AK2 + KC2 =22 + 32 = 13.
- Trong tam giác BCI có: BC2 = BI2 + IC2 = 12 + 52 =26.
Nhận thấy AB2 = AC2 ⟹ AB = AC nên ∆ABC cân tại A (1)
Áp dụng định lý Pytago đảo ta thấy AB2 + AC2 = BC2 nên ∆ABC vuông tại A (2)
Từ (1) và (2) suy ra ∆ABC vuông cân tại A.