Cho đường tròn (O) và đường thẳng d không cắt (O). Hãy dựng tiếp tuyến của (O) sao cho tiếp tuyến đó song song vói d
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 3 2019
* Phân tích
Giả sử tiếp tuyến của đường tròn dựng được thỏa mãn điều kiện bài toán
- d 1 là tiếp tuyến của đường tròn tại A nên d 1 ⊥ OA
- Vì d 1 // d nên d ⊥ OA
Vậy A là giao điểm của đường thẳng kẻ từ O vuông góc với d
* Cách dựng
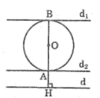
- Dựng OH vuông góc với d cắt đường tròn (O) tại A và B
- Dựng đường thẳng d 1 đi qua A và vuông góc với OA
- Dựng đường thẳng d 2 đi qua B và vuông góc với OB
Khi đó d 1 và d 2 là hai tiếp tuyến cần dựng.
* Chứng minh
Ta có: A và B thuộc (O)
d 1 // d mà d ⊥ OH nên d 1 ⊥ OH hay d 1 ⊥ OA tại A
Suy ra d 1 là tiếp tuyến của đường tròn (O)
d 2 // d mà d ⊥ OH nên d 2 ⊥ OH hay d 2 ⊥ OB tại B
Suy ra d 2 là tiếp tuyến của đường tròn (O)
* Biện luận
Đường thẳng OH luôn cắt đường tròn (O) nên giao điểm A và B luôn dựng được.
7 tháng 10 2023
a: Xét (O) có
DB,DC là tiếp tuyến
=>DB=DC
DB=DC
OB=OC
Do đó: OD là đường trung trực của BC
=>OD vuông góc BC
b: Xét (O) có
DB,DC là tiếp tuyến
Do đó: DO là phân giác của góc CDB
BC//GE
DO vuông góc BC
Do đó: DO vuông góc GE
Xét ΔDGE có
DO vừa là đường cao, vừa là đường phân giác
Do đó: ΔDGE cân tại D
=>DG=DE
ΔDGE cân tại D
mà DO là đường cao
nên O là trung điểm của GE
=>OG=OE
c: OG//BC
=>góc AOG=góc ABC(đồng vị) và góc COG=góc OCB(hai góc so le trong)
mà góc ABC=góc OCB
nên góc AOG=góc COG
=>OG là phân giác của góc COA
Xét ΔOCG và ΔOAG có
OC=OA
góc COG=góc AOG
OG chung
Do đó: ΔOCG=ΔOAG
=>góc OAG=góc OCG=90 độ
=>AG là tiếp tuyến của (O)
20 tháng 1 2023
1: Xét ΔBDA có
O là trung điẻm của AB
OI//BD
=>I là trung điểm của AD
ΔOAD cân tại O
mà OI là trung tuyến
nên OI vuông góc AD và OI là phân giác của góc AOD
2: Xét ΔOAC và ΔODC có
OA=OD
góc AOC=góc DOC
OC chung
Do đó: ΔOAC=ΔODC
=>góc ODC=90 độ
=>CD là tiếp tuyến của (O)
CM
1 tháng 11 2017
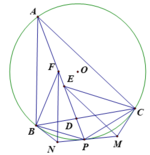
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.
2 tháng 12 2023
a: Sửa đề: cắt tiếp tuyến tại A của đường tròn ở C
ΔOAB cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OAC}=\widehat{OBC}=90^0\)
=>CB là tiếp tuyến của (O)
b:ΔOAC=ΔOBC
=>CB=CA
=>C nằm trên đường trung trực của AB(1)
OA=OB
=>O nằm trên đường trung trực của AB(2)
từ (1) và (2) suy ra OC là đường trung trực của BA
=>OC\(\perp\)AB
mà OC//AD
nên AB\(\perp\)AD
=>ΔABD vuông tại A
Ta có: ΔABD vuông tại A
=>ΔABD nội tiếp đường tròn đường kính DB
mà ΔABD nội tiếp (O)
nên O là trung điểm của DB
=>D,O,B thẳng hàng
Xét ΔAKD vuông tại K và ΔCAO vuông tại A có
\(\widehat{ADK}=\widehat{COA}\)(hai góc so le trong, AD//CO)
Do đó: ΔAKD\(\sim\)ΔCAO
CM
18 tháng 2 2018
2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .
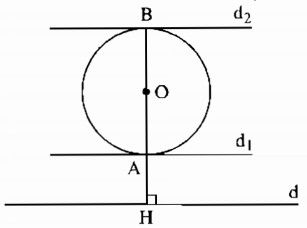
Từ O hạ OH vuông góc với d. OH cắt (O) tại A và B. Qua A và B kẻ các đường vuông góc với OA và OB ta được hai (hoặc một nếu d là tiếp tuyến của (O)) tiếp tuyến song song với d.