Cho tam giác ABC có BC = 11 cm, A B C ^ = 38 0 và A C B ^ = 30 0 . Gọi N là chân đường vuông góc hạ từ A xuông cạnh BC. Hãy tính:
a, Độ dài đoạn thẳng AN
b, Độ dài đoạn thang AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 3 2019
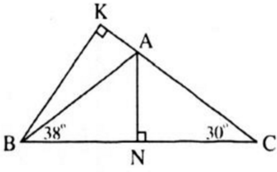
Kẻ BK ⊥ AC (K ∈ AC).
Trong tam giác vuông BKC có:
∠ K B C = 9 ° o – 30 ° = 60 ° = > ∠ K B A = 60 ° – 38 ° = 22 °
BC = 11 (cm) => BK = 5,5 (cm) ( tính chất cạnh đối diện góc 30° trong tam giác vuông bằng nửa cạnh huyền )
Xét tam giác ABK vuông tại K:
Xét tam giác ANB vuông tại N:
=> AN = ABsinABN = 5,93.sin38° ≈ 3,65(cm)
b) Xét tam giác ANC vuông tại N:
23 tháng 7 2017
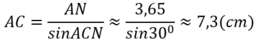
a) +Xét tam giác ABD :
ta có góc B = 60* ,góc BAD = 60*
mà góc B + góc BAD + ADB = 180* ( tổng 3 góc )
=> góc ADB = 60*
=> tam giac ABD là tam giác đều ( mỗi góc = 60*) => AB = BD = AD = 7cm
ta có H là trung diem BD => AH là duong trung tuyến,là tia phan giac goc BAD,là duong cao cùa tam giac ABD ( tam giac ABD đều ) => HD = HB = 1/2 BD = 3.5cm
+áp dụng định lí pitago vào tam giác ABH vuong tai H có AB = 7cm,BH = 3.5 cm :
AB^2 = AH^2 + BH^2 => em tự tính AH nhé
+ta có BH + HC = BC => HC = BC - HB = 15 - 3.5 = 11.5cm
+áp dụng dinh li pitago vào tam giac vuong AHC vuong tai H có AH ( lúc nãy tính ) và HC = 11.5cm
AC^2 =AH^2 + HC^2 => AC =13cm
b) AB ^2 + AC^2 có = BC ^2 ko? nếu = thì tam giac ABC vuong tai A
15 tháng 11 2015
a)Góc MAN =60+60+60 =180 => M,A,N thẳng hàng
b)Xét tam giác ABN và AMC : có AB=AM ; góc NAB = góc CAM =120; AN = AC
=> ABN =AMC ( c-g-c)
=> BN =MC cạnh tương ứng
c)Gọi K là giao điểm AB và MC
Xét 2 tam giác KAM và KOB
theo b =>góc M = góc B
H1 = H2 đối đỉnh
=> A=O =60
Mà O+ BOC =180=> BOC =180 -60 =120
CT
23 tháng 12 2021
vậy bạn làm câu d của bài này giúp mình nhé
cho tam giác ABC có góc A bằng 60 độ. vẽ ngoài tam giác ABC các tam giác đều là ABM và ACN. gọi giao điểm của BN và CM là O. chứng minh OA là tia phân giác của góc MON
VT
0
28 tháng 9 2018
kẻ BK vuongAC ^CBK vuong tai K và ^C = 30 độ = > tam giácCBK nửa đều BK = BC/2 = 5,5 ^KBC = 180-(BKA+^C) = 60độ ^KBA = ^KBC-^ABC = 22 độ = >tam giác KBA có KBA = 22 độ = >AB = BK:sinKBA = 5,5:sin22 = 5,93194 AN = AB.sinABN = 3,65207 b) AC = 2AN = 7,30414
HH
16 tháng 8 2020
Kẻ \(BK\perp AC\left(K\in AC\right)\)
Trong tam giác vuông BKC có:
\(\widehat{KBC}=60^o-30^o=60^o\)
\(\Rightarrow\widehat{KBA}=60^o-38^o=22^o\)
BC = 11 (cm) => BK = 5,5 (cm) ( tính chất cạnh đối diện góc 30° trong tam giác vuông bằng nửa cạnh huyền )
Xét tam giác ABK vuông tại K : \(\cos KBA=\frac{BK}{AB}\)
\(\Rightarrow AB=\frac{BK}{\cos KBA}=\frac{5,5}{\cos22^o}\approx5,93\left(cm\right)\)
Xét tam giác ANB vuông tại N : \(\sin ABN=\frac{AN}{AB}\)
\(\Rightarrow AN=AB\sin ABN=5,93.\sin38^o\approx3,65\left(cm\right)\)
b) Xét tam giác ANC vuông tại N : \(\sin ACN=\frac{AN}{AC}\)
\(AC=\frac{AN}{\sin ACN}\approx\frac{3,65}{\sin30^o}\approx7,3\left(cm\right)\)
4 tháng 8 2016
a) \(\Delta ADE=\Delta ADF\) (cạnh huyền - góc nhọn) \(\Rightarrow\)\(AE=AF\)và góc ADE = góc ADF, DE = DF.
b) Do CM // AD nên \(\Delta BAD\) đồng dạng \(\Delta BMC\)(hệ quả định lý Ta-lét) \(\Rightarrow\)\(\frac{BD}{CD}=\frac{AB}{AM}\)
Mà \(\frac{BD}{CD}=\frac{AB}{AC}\)(AD là phân giác) \(\Rightarrow\) \(\frac{AB}{AC}=\frac{AB}{AM}\)\(\Rightarrow\)AC = AM nên \(\Delta ACM\)cân tại A.
\(\Delta ACM\)cân tại A có góc MAC = 1800 - góc BAC = 1800 - 1200 = 600 nên \(\Delta ACM\)đều.
c) Gọi O là giao điểm EF và AD.
\(\Delta ODE\) và \(\Delta ODF\) có: cạnh OD chung, góc ADE = góc ADF và DE = DF \(\Rightarrow\)\(\Delta ODE=\Delta ODF\)(c-g-c)
\(\Rightarrow\)góc \(EOD=FOD=90^0\)\(\Rightarrow\)AD vuông góc EF mà CM // AD \(\Rightarrow\)EF vuông góc CM.
4 tháng 8 2016
Mình nghĩ đề đúng phải là:
Cho tam giác ABC có góc A = 1200 , đường phân giác AD, E và F là chân đường vuông góc kẻ từ D xuống AB và AC.
a) Chứng minh: AE=AF
b) kẻ CM // AD, M thuộc AB. Tam giác AMC là tam giác gì ?
c) Chứng minh: EF vuông góc với CM
a, Cách 1. Sử dụng các tỉ số lượng giác trong tam giác vuông NAB và NAC chúng ta có BN.tanB = NC.tanC
Chú ý BN + NC = BC chúng ta tính được
BN ≈ 4,67cm => AN ≈ 3,65cm
Cách 2. Gợi ý: Kẻ CH vuông góc với AB tại H
b, Xét ∆ANC vuông có: A C = A N sin C => AC ≈ 7,3cm