Một người đứng ngắm một cái cửa cách xa 5 m. Cửa cao 2 m. Tính độ cao của ảnh cửa trên màng lưới của mắt. Coi thể thủy tinh như một thấu kính hội tụ, cách màng lưới 2 cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
16 tháng 5 2017
Trên hình ta biểu diễn cột điện bằng đoạn AB (AB = 8 cm); O là thể thủy tinh (OA = 20 m); A'B' là ảnh cột điện trên màng lưới (OA' = 2 cm). Ta có:
= 
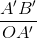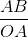=> A'B' = 
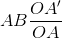= 0,8 cm
25 tháng 3 2022
Khoảng cách từ thể thủy tinh đến màng lưới là \(d'=2cm\)
Cái cây quan sát được cách mắt một đoạn \(d=25m=2500cm\)
Ảnh hiện trên màng lưới \(h'=0,8cm\)
Chiều cao của cây:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{h}{0,8}=\dfrac{2500}{2}\Rightarrow h=1000cm=10m\)
VT
9 tháng 5 2019
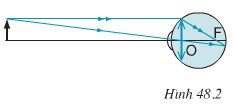
Quá trình tạo ảnh của thể thủy tinh được mô phỏng bằng hình vẽ sau: (coi màn PQ như màng lưới trên võng mạc của mắt).
Ký hiệu cột điện là AB, ảnh của cột điện trên màng lưới là A’B’, thể thủy tinh là thấu kính hội tụ đặt tại O. Ta có: AO = 20m = 2000cm; A’O = 2cm; AB = 8m = 800cm.
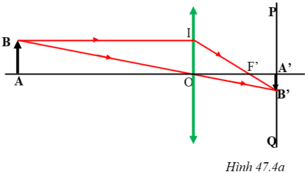
Hai tam giác ABO và A’B’O đồng dạng với nhau, ta có:
Chiều cao của ảnh cột điện trên màng lưới là:
VT
27 tháng 5 2019
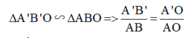
Chiều cao ảnh của cây trong màng lưới mắt Hằng là:
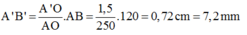
→ Đáp án A
VT
17 tháng 11 2017
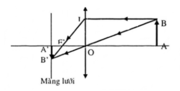
Quá trình tạo ảnh của thể thủy tinh được mô phỏng bằng hình vẽ sau: (coi màn PQ như màng lưới trên võng mạc của mắt)
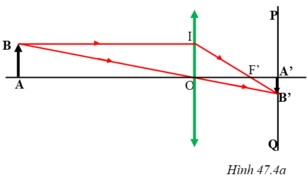
- Hai tam giác ABO và A’B’O đồng dạng với nhau, ta có:
Vì khoảng cách từ thể thủy tinh của mắt đến màng lưới là không thay đổi và ảnh của vật luôn hiện rõ nét trên màng lưới nên ta có AB và OA' không đổi
→ nếu OA lớn (vật ở càng xa mắt) thì ảnh A’B' nhỏ và ngược lại.
- Hai tam giác OIF và A'B'F đồng dạng, nên:
Hay:
Vì OA' và AB không đổi, nên nếu A'B' nhỏ thì OF’ lớn và ngược lại.
Kết quả là nếu OA càng lớn thì A'B' càng nhỏ, OF càng lớn và ngược lại. Nghĩa là khi nhìn các vật ở càng xa thì tiêu cự của mắt càng lớn, khi nhìn các vật càng gần thì tiêu cự của mắt càng nhỏ.
N
30 tháng 4 2022
Ta có: \(OA'=d'=2cm\), người này quan sát thấy cái tháp cao 5m nên \(h=5m=500cm\) và khoảng cách từ tháp đến người này là 30 cm nên \(d=30cm\).
Chiều cao của ảnh trên màng lưới:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow h'=\dfrac{h\cdot d'}{d}=\dfrac{500\cdot2}{30}\approx33,\left(3\right)cm\)
VT
21 tháng 11 2017
d=20m
d′=2cm=0,02m
h=10m
Ta có:
h h ' = d d ' → h ' = d ' d h = 0 , 02 20 . 10 = 0 , 01 m = 1 c m
Đáp án: B
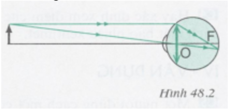
Dựa vào hình trong bài 23, coi PQ là màng lưới của mắt.
OA là khoảng cách từ mắt đến cửa: OA = d = 5m = 500cm
OA’ là khoảng cách từ thể thủy tinh đến màng lưới: OA’ = d’ = 2cm
AB là cái cửa: AB = h = 2m = 200cm
A’B’ là ảnh của cái cửa trên màng lưới
Trên hình vẽ, xét cặp tam giác đồng dạng: ΔABO và ΔA’B’O
Từ hệ thức đồng dạng được: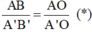
Từ (*) ta được độ cao của ảnh cửa trên màng lưới là: