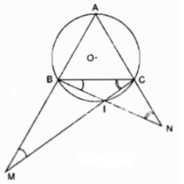
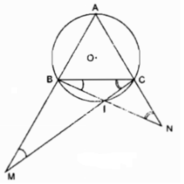
Cho đường tròn tâm O bán kính R. Lấy 3 điểm A, B, C trên đường tròn đó sao cho AB = BC = CA. Gọi I là điểm bất kỳ của cung nhỏ BC (và I không trùng với B, C). Gọi M là giao điểm của CI và AB. Gọi N là giao điểm của BI và AC. Chứng minh: ∠ ANB = ∠ BCI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CM
Cao Minh Tâm
24 tháng 8 2018

Đúng(0)
Những câu hỏi liên quan

11 tháng 2 2023
a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
=>ΔAMB vuông tại M
Xét tứ giác BMIJ có
góc IJB+góc IMB=180 độ
=>BMIJ là tứ giác nội tiếp
b: BMIJ là tứgiác nội tiếp
=>góc MJI=góc MBI
Xét tứ giác CAJI có
góc ACI+góc AJI=180 độ
=>CAJI là tứ giác nội tiêp
=>góc CJI=góc CAI
góc MJI=góc MBI
mà góc CAI=góc MBI
nên góc CJI=góc MJI
=>JI là phân giác của góc CJM

12 tháng 5 2023
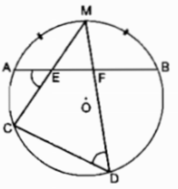
a: góc AEB=1/2*180=90 độ
góc FIB+góc FEB=180 độ
=>FIBE nội tiếp
b: góc ACB=1/2*180=90 độ
=>AC vuông góc DB
Xét ΔCAF và ΔCEA có
góc CAF=góc CEA
góc ACF chung
=>ΔCAF đồng dạng với ΔCEA
=>CA^2=AF*AE
Xét ΔDAB vuông tại D có AC vuông góc DB
nên CA^2=CD*CB=AF*AE