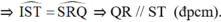Xem hình 48. Chứng minh QR // ST.
Hướng dẫn: Xét cặp góc so le trong P S T ^ , S R Q ^
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Các cặp góc sole trong là : S3 và R2 ; S4 và R1
Các cặp góc đồng vị là : S1 và R1; S2 và R2; S3 và R4; S4 và R3
Các góc trong cùng phía là : S3 và R1; S4 và R2
b) R4 = S3 = 120\(\)o (2 góc đồng vị)
R4 = R2 = 120o (2 góc đối đỉnh)
R2 + R1 = 180o (2 góc kề bù)
⇒ 120o + R1 =180o
⇒ R1 = 180o - 120o
⇒ R1 = 60o
R1 = S1 = 60o (2 góc đồng vị)
R1 = R3 = 60o (2 góc đối đỉnh)
S1 = S4 = 60o (2 góc đối đỉnh)

Đúng rùi anh, đọc cái đề không biết dễ hay khó nhưng nhìn vào nản không muốn làm. Hì

Các cặp góc đồng vị và so le trong và so le ngoài luôn bằng nhau
Còn các cặp góc trong cùng phía và ngoài cùng phía thì bù nhau

R A M B H Q C D S N P
a) Xét tam giác vuông ABR và ADQ có:
AB = AD (gt)
Góc BAR + góc BAP = 90 độ
Góc DAQ + góc BAP = 90 độ
=> Góc BAR = Góc DAQ
=> Tam giác vuông ABR = tam giác vuông ADQ (cạnh góc vuông – góc nhọn kề)
=> AR = AQ (2 cạnh tương ứng)
=> Tam giác AQR cân tại A.
CMTT ta có tam giác ADS = tam giác ABP
=> AS = AP => Tam giác APS cân tại A.
b) Tam giác AQR cân tại A => Trung tuyến AM đồng thời là đường cao.
=> AM vuông góc với QR => Góc AMH = 90 độ
Tương tự: Tam giác APS cân tại A => Trung tuyến AN đồng thời là đường cao.
=> AN vuông góc với SP => góc ANP = 90 độ hay góc ANH= 90 độ.
Tam giác AQR vuông cân tại A => Góc AQR = góc ARQ = 45 độ => Góc PQH = 45 độ.
Tam giác APS vuông cân tại A => góc ASP = góc APS = 45 độ => góc QPH = 45 độ (đối đỉnh).
Xét tam giác PHQ có: Góc PQH + góc QPH = 45 độ + 45 độ = 90 độ
=> Tam giác PHQ vuông cân tại H => PH vuông góc với PQ
=> góc NHM = 90 độ
Xét tứ giác AMHN có: Góc AMH = góc ANH = góc NHM = 90 độ
=> AMHN là hình chữ nhật (dhnb)
c) Xét tam giác SQR có:
BC vuông góc CD => RC vuông góc SQ => RC là đường cao.
AP vuông góc AR => QA vuông góc RS => QA là đường cao.
Mà RC cắt QA tại P
Vậy P là trực tâm tam giác SQR.
d) Tam giác ANP vuông tại A có trung tuyến AN => AN = SP/2
Tam giác CSP vuông tại C có trung tuyến CN => CN = SP/2
=> AN = CN => N thuộc trung trực của AC.
CMTT ta có MA = MC => M thuộc trung trực của AC.
Vậy MN là trung trực của AC.
e) Ta có BA = BC (gt) => B thuộc trung trực của AC.
Mà MN là trung trực của AC (cmt) => B thuộc MN
Tương tự DA = DC (gt) => D thuộc trung trực của AC.
Mà MN là trung trực của AC (cmt) => D thuộc MN
Vậy M, B, N, D thẳng hàng.
Từ (1);(2);(3)