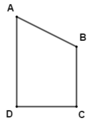
Cho hình bên:
Cạnh AD song song với cạnh nào dưới đây ?
A. BC
B. AB
C. CD
D. DA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Gọi K là giao của AD và BC
Xét ΔKDC có AB//DC
nên KA/AD=KB/BC
=>KA/KB=AD/BC
Xét ΔKMN có AB//MN
nên KA/AM=KB/BN
=>KA/KB=AM/BN
=>AM/BN=AD/BC
=>AM/AD=BN/BC
b: AM/AD=BN/BC
=>AD/AM=BC/BN
=>AD/AM-1=BC/BN-1
=>\(\dfrac{AD-AM}{AM}=\dfrac{BC-BN}{BN}\)
=>DM/AM=NC/BN
=>MA/MD=BN/NC
c: AM/AD=BN/BC
=>AM/AD-1=BN/BC-1
=>(AM-AD)/AD=(BN-BC)/BC
=>-MD/AD=-CN/BC
=>MD/AD=CN/BC

Quan sát hình vẽ ta thấy cạnh AB song song với cạnh DC.
Đáp án B

a) Cạnh AB bằng cạnh DC
b) Cạnh AD bằng cạnh BC
c) Cạnh AB song song với cạnh DC
d) Cạnh AD song song với cạnh BC

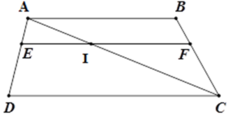
Gọi I là giao điểm của AC với EF.
Xét ΔADC có EI // DC, theo định lý Ta-lét ta có: A E A D = A I A C (1)
Xét ΔABC có IF // AB, theo định lý Ta-lét ta có: A I A C = B F B C (2)
Từ (1) và (2) suy ra A E A D = B F B C
⇒ E D A D + B F B C = E D A D + A E A D = E D + A E A D = A D A D = 1
Do đó E D A D + B F B C = 1 hay A đúng
Đáp án: A
Chọn A. BC