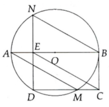
Cho (O) đường kính AB. Vẽ hai dây AM và BN song song với nhau sao cho Sđ cung BM<90°. Vẽ dây MD song song với AB. Dây DN cắt AB tại E. Từ E vẽ 1 đường thẳng // với AM cắt DM tại C. CMR:
a) AB vuông góc DN.
b) BC là tiếp tuyến (O).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 3 2019
a, HS tự chứng minh
b, Ta chứng minh được tứ giác BCEN là hình bình hành => BC = EN
Do BCDE là hình bình hành
=> BC = ED; DE = EN
=> BA ⊥ EN => BABC
=> BC là tiếp tuyến
16 tháng 4 2020
a) Ta có \(\widehat{AND}=\widehat{AMD}\)(góc nội tiếp cùng chắn cung AD)
\(AM//BN\Rightarrow\widehat{AMN}=\widehat{MNB}\left(slt\right)\)
Ta có góc ANB nội tiếp đường trong O chắn nửa đường trong => góc ANB=900
Ta có: \(\widehat{AMD}+\widehat{AMN}+\widehat{DNM}=\widehat{DNM}+\widehat{AND}+\widehat{MNB}\)
\(\Leftrightarrow\widehat{DMN}+\widehat{MND}=90^0\Leftrightarrow\widehat{NDM}=90^0\)
Vì DM//AB và ND vuông góc với DM => DN vuông góc với AB
b) Ta có \(\widehat{BAN}=\widehat{BMN}\)(cùng chắn cung BN)
Mà \(\widehat{AMN}+\widehat{NMB}=90^0\Rightarrow\widehat{BAN}+\widehat{BAM}=90^0\Rightarrow\widehat{MAN}=90^0\)
\(\Rightarrow MANB\)là hcn
=> AM=BN
Ta có MC//AE và AM//EC => AMCE là hbh => AM=EC mà AM=BN => BN=EC mà BN//EC => ENBC là hbh =>EN//CB => CB vuông góc với AB(vì AB vuông góc với EN)=> BC là tiếp tuyến của đường tròn O
Chúc bạn học tốt!!!
9 tháng 2 2023
a: AM//BN
=>AMBN là hình thang
=>góc MAN+góc ANB=180 độ
=>góc NAM=góc AMB
=>AN//MB
mà AM//BN
nên AMBN là hình bình hành
=>BM=AD và AB cắt MN tại trung điểm của mỗi đường
=>O là trung điểm của MN
b: MD//AB
Xét ΔMDN có
góc MDN là góc nội tiếp chắn nửa đường tròn
=>góc MDN=90 độ
=>MD vuông góc DN
=>DN vuông góc AB
c: ΔODN cân tại O
mà OE là đường cao
nên E là trung điểm của DN
=>DE=EN