ho biết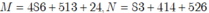 
. Không tính kết quả hãy so sánh M, N
A. M>N
B. M<N
C. M=N
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
3
IW
19 tháng 11 2016
Xét A ta có: A=m*(n+1)
=> A=m*n+m
Xét B ta có: B=n*(m+n)
=> B=n*m+n*n
nên xem lại đề bạn ạ! Đề của bạn cho thiếu dữ liệu
LD
2
M
23 tháng 7 2016
Dễ:
M=1999x(2000+1) N=2000x(1999+1)
M=1999x2000+1999x1 N=2000x1999+2000x1
Ta có:1999x1<2000x1
Cả M và N đều có chung 1999x2000
Suy ra M<N
23 tháng 7 2016
Ta có M = 1999 x 2001 = 1999 x ( 2000 + 1)
suy ra M = 1999 x 2000 + 1999 (1)
Mặt khác : N = 2000 x 2000 = 2000 x ( 1999 + 1 )
suy ra : N = 2000 x 1999 + 2000 (2)
Từ ( 1) và (2) suy ra N > M
Từ (1) và (2) suy ra N >
LY
0
V
0
14 tháng 8 2023
a: \(log_2\left(mn\right)=log_2\left(2^7\cdot2^3\right)=7+3=10\)
\(log_2m+log_2n=log_22^7+log_22^3=7+3=10\)
=>\(log_2\left(mn\right)=log_2m+log_2n\)
b: \(log_2\left(\dfrac{m}{n}\right)=log_2\left(\dfrac{2^7}{2^3}\right)=7-3=4\)
\(log_2m-log_2n=log_22^7-log_22^3=7-3=4\)
=>\(log_2\left(\dfrac{m}{n}\right)=log_2m-log_2n\)
D
datcoder
CTVVIP
14 tháng 8 2023
a) \(\log_2\left(mn\right)=\log_2\left(2^7.2^3\right)=\log_22^{7+3}=\log_22^{10}=10.\log_22=10.1=10\)
\(\log_2m+\log_2n=\log_22^7+\log_22^3=7\log_22+3\log_22=7.1+3.1=7+3=10\)
b) \(\log_2\left(\dfrac{m}{n}\right)=\log_2\dfrac{2^7}{2^3}=\log_22^4=4.\log_22=4.1=4\)
\(\log_2m-\log_2n=\log_22^7-\log_22^3=7.\log_22-3\log_22=7.1-3.1=4\)
9 tháng 5 2016
M=(2006-1)x(2006+1)=2006x2006-2006+2006-1=2006x2006-1
M=2006x2006-1
N=2006x2006
Vậy M<N
VN
Võ Ngọc Phương
VIP
13 tháng 9 2023
b) \(M=\dfrac{10^{2023}+1}{10^{2024}+1}< 1\) ( Vì tử < mẫu )
Ta có: \(M=\dfrac{10^{2023}+1}{10^{2024}+1}< \dfrac{10^{2023}+1+9}{10^{2024}+1+9}=\dfrac{10^{2023}+10}{10^{2024}+10}=\dfrac{10.\left(10^{2022}+1\right)}{10.\left(10^{2023}+1\right)}=\dfrac{10^{2022}+1}{10^{2023}+1}=N\)
Vì \(\dfrac{10^{2023}+1}{10^{2024}+1}< \dfrac{10^{2022}+1}{10^{2023}+1}\) nên \(M< N\)
Đáp án C