Cho các số hữu tỉ: - 2 3 ; - 3 5 ; 2 3 ; 5 4 ; 0 . Hãy sắp xếp các số hữu tỉ trên theo thứ tự tăng dần:
A. - 2 3 ; - 3 5 ; 0 ; 5 4 ; 2 3
B. - 3 5 ; - 2 3 ; 0 ; 5 4 ; 2 3
C. - 3 5 ; - 2 3 ; 0 ; 2 3 ; 5 4
D. - 2 3 ; - 3 5 ; 0 ; 2 3 ; 5 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có:
\(\dfrac{-2}{3}=\dfrac{-40}{60}\)
\(\dfrac{-3}{5}=\dfrac{-36}{60}\)
\(\dfrac{2}{3}=\dfrac{40}{60}\)
\(\dfrac{5}{4}=\dfrac{75}{60}\)
→ \(\dfrac{-40}{60}< \dfrac{-36}{60}< 0< \dfrac{40}{60}< \dfrac{75}{60}\)
Hay : \(\dfrac{-2}{3}< \dfrac{-3}{5}< 0< \dfrac{2}{3}< \dfrac{5}{4}\)
Chúc bạn học tốt
Các số hữu tỉ âm là :
\(\frac{-3}{7};\frac{1}{-5};-4\)
CÁc số không phải số hữ tỉ âm + giải thích là :
\(\frac{2}{3}>0\)
\(\frac{0}{-2}=0\)( không là số hữu tỉ âm cũng không là số hữu tỉ dương )
\(\frac{-3}{-5}=\frac{3}{5}>0\)
- Số hữu tỷ dương: \(\frac{2}{3}\)
- Số hữu tỷ âm: \(\frac{-3}{7};\frac{-1}{5};-4;\frac{-3}{5}\)
- Số không phải số hữu tỷ âm cũng không phải số hữu tỷ dương: \(\frac{0}{-2}\)
- Số 3/0 không phải là số hữu tỷ.
Lời giải:
Đặt $x+\frac{2}{3}=\frac{a}{b}$ với $a,b$ là số nguyên, $b\neq 0$
$\Rightarrow x=\frac{a}{b}-\frac{2}{3}=\frac{3a-2b}{3b}$
Thấy rằng $3a-2b\in\mathbb{Z}$ với mọi $a,b$ nguyên, $3b\in\mathbb{Z}\neq 0$ với mọi số nguyên $b$ khác $0$
$\Rightarrow x$ là số hữu tỉ.
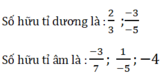
Số hữu tỉ không là số hữu tỉ dương cũng không là số hữu tỉ âm là: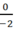 
- Vì \(0,6=\frac{6}{10}=\frac{3}{5}\)
\(-1,25=\frac{-125}{100}=\frac{-5}{4}\)
nên 0,6 và -1,25 là các số hữu tỉ
- Số nguyên a là số hữu tỉ vì ta có thể viết a dưới dạng phân số là \(\frac{\alpha}{1}\)
- Câu c bạn tự vẽ nha
- số hữu tỉ dương : \(\frac{2}{3};\frac{-3}{-5}\)
số hữu tỉ âm : \(\frac{-3}{7};\frac{1}{-5};-4\)
số không hữu tỉ âm cũng không phải hữu tỉ dương là \(\frac{0}{-2}\) ( vì kết quả bằng 0 )
a) Các số hữu tỉ dương là: \(\frac{5}{{12}};\,2\frac{2}{3}.\)
Các số hữu tỉ âm là: \( - \frac{4}{5}; - 2;\, - 0,32.\)
Số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: \(\frac{0}{{234}}\).
b) Ta có: \( - \frac{4}{5} = -0,8\)
Vì 0 < 0,32 < 0,8 < 2 nên 0 > -0,32 > -0,8 > -2 hay \(-2 < - \frac{4}{5} < -0,32 < 0\)
Mà \(0 < \frac{5}{12} <1; 1<2\frac{2}{3}\) nên \(0 < \frac{5}{12} < 2\frac{2}{3}\)
Các số theo thứ tự từ nhỏ đến lớn là:
\(-2 ; - \frac{4}{5} ; -0,32; \frac{0}{{234}}; \frac{5}{12} ; 2\frac{2}{3}\)
Chú ý: \(\frac{0}{a} = 0\,,\,a \ne 0.\)
a) +) Ta có: \( - 3,75 = \frac{{ - 375}}{{100}} = \frac{{ - 15}}{4} = \frac{{ - 45}}{{12}}\).
Do \( - 7 > - 45\) nên \(\frac{{ - 7}}{{12}} > \frac{{ - 45}}{{12}}\).
+) Ta có: \(\frac{0}{{ - 3}} = 0\). Nên \(\frac{0}{{ - 3}} < \frac{4}{5}\).
b) Các số hữu tỉ dương là: \(\frac{4}{5};\,5,12\).
Các số hữu tỉ âm là: \(\frac{{ - 7}}{{12}};\, - 3;\, - 3,75\)
Do \(\frac{0}{{ - 3}} = 0\) nên số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: \(\frac{0}{{ - 3}}\).
Ta có \(9x-4y=\left(3\sqrt{x}-2\sqrt{y}\right)\left(3\sqrt{x}+2\sqrt{y}\right)\)là số hữu tỷ
Vì \(\left(3\sqrt{x}-2\sqrt{y}\right)\)(1) là số hữu tỷ nên \(\left(3\sqrt{x}+2\sqrt{y}\right)\)(2) cũng là số hữu tỷ
Lấy (2) - (1) và (2) + (1) ta được
\(\hept{\begin{cases}4\sqrt{y}\\6\sqrt{x}\end{cases}}\)là 2 số hữu tỷ vậy \(\sqrt{x},\sqrt{y}\)là hai số hữu tỷ
Ta có:
Chọn đáp án D