Câu 1: Phương trình (3,5x−7)(2,1x−6,3)=0 có tổng các nghiệm bằngA:6 B:3 C:5 D:4Câu 2: Nghiệm của phương trình 4(3x−2)−3(x−4)=7x+20 là x=a.Chọn khẳng định đúng:A:6<a<=8 B:5<a<7 C:7<a<8 D:8<a<=10 Câu 3: Tập nghiệm của phương trình (x−2)(x+2)=0 là...
Đọc tiếp
Câu 1: Phương trình (3,5x−7)(2,1x−6,3)=0 có tổng các nghiệm bằng
A:6 B:3 C:5 D:4
Câu 2: Nghiệm của phương trình 4(3x−2)−3(x−4)=7x+20 là x=a.
Chọn khẳng định đúng:
A:6<a<=8 B:5<a<7 C:7<a<8 D:8<a<=10
Câu 3: Tập nghiệm của phương trình (x−2)(x+2)=0 là :
A:S={-2;2} B:S={2} C:S={vô nghiệm} D:S={-2}
Câu 4: Tổng giá trị các nghiệm của hai phương trình bên dưới là:
(x^2+x+1)(6−2x)=0 và (8x−4)(x^2+2x+2)=0
A:13/5 B:13/2 C:7/2 D:13/3
Câu 5: Các giá trị k thỏa mãn phương trình (3x+2k−5)(x−3k+1)=0 có nghiệm x=1 là:
A:k=2 và k=1 B:k=3 và k=1/2 C:k=1 và k=2/3 D:k=2 và k=1/3
Câu 6: Tập nghiệm của phương trình x^2+3x−4=0 là
A:S={-4;1} B:S={vô nghiệm} C:S={-1;4} D:S={4;1}
Câu 7: Phương trình (3x−2)(2(x+3)/7−(4x−3)/5)=0 có 2 nghiệm x1,x2 Tích x1.x2 có giá trị bằng
A:x1.x2=17/3 B:x1.x2=5/9 C:x1.x2=17/9 D:x1.x2=17/6
Câu 8: Cho phương trình (x−5)(3−2x)(3x+4)=0 và (2x−1)(3x+2)(5−x)=0 .
Tổng giá trị các nghiệm của 2 phương trình trên là:
A:11 B:9 C:12 D:10
Câu 9: Phương trình (3−2x)(6x+4)(5−8x)=0. Nghiệm lớn nhất của phương trình là:
A:x=2/3 B:x=8/5 C:x=3/2 D:x=5/8
Câu 10: Phương trình (4x−10)(24+5x)=0 có nghiệm là:
A:x=5/2 và x=24/5 B:x=-5/2 và x=-24/5 C:x=5/2 và x=-24/5
D:x=-5/2 và x=24/5
= 0.
.
.
.
.
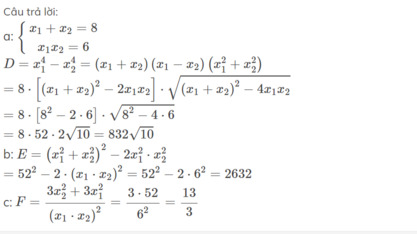
Đáp án D
Ta có: a = 1; b = - 8 nên b’ = -4; c = 10.
△ ' = - 4 2 - 1.10 = 16 - 10 = 6
Do đó, phương trình đã cho có hai nghiệm phân biệt là;
Vậy cả hai nghiệm trên đều là nghiệm dương của phương trình đã cho.